【题目】已知![]() R,命题
R,命题![]() :对任意
:对任意![]() ,不等式
,不等式![]() 恒成立;命题
恒成立;命题![]() :存在
:存在![]() ,使得
,使得![]() 成立.
成立.
(1)若![]() 为真命题,求
为真命题,求![]() 的取值范围;
的取值范围;
(2)若![]() 且
且![]() 为假,
为假, ![]() 或
或![]() 为真,求
为真,求![]() 的取值范围;
的取值范围;
参考答案:
【答案】(1)[1,2] (2)(-∞,1)∪(1,2]
【解析】试题分析:(1)由对任意![]() ,不等式
,不等式![]() 恒成立,知
恒成立,知![]() ,由此能求出
,由此能求出![]() 的取值范围;(2)存在
的取值范围;(2)存在![]() ,使得
,使得![]() 成立,推导出命题
成立,推导出命题![]() 满足
满足![]() ,由
,由![]() 且
且![]() 为假,
为假, ![]() 和
和![]() 为真,知
为真,知![]() 、
、![]() 一真一假,分两种情况讨论,对于
一真一假,分两种情况讨论,对于![]() 真
真![]() 假以及
假以及![]() 假
假![]() 真分别列不等式组,分别解不等式组,然后求并集即可求得实数
真分别列不等式组,分别解不等式组,然后求并集即可求得实数![]() 的取值范围.
的取值范围.
试题解析:(1)∵对任意x∈[0,1],不等式2x-2≥m2-3m恒成立,
∴(2x-2)min≥m2-3m.即m2-3m≤-2.解得1≤m≤2.
因此,若p为真命题时,m的取值范围是[1,2].
(2)存在x∈[-1,1],使得m≤x成立,∴m≤1,
命题q为真时,m≤1.∵p且q为假,p或q为真,
∴p,q中一个是真命题,一个是假命题.
当p真q假时,则![]() 解得1<m≤2;
解得1<m≤2;
当p假q真时, ![]() 即m<1.
即m<1.
综上所述,m的取值范围为(-∞,1)∪(1,2].
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,F为弦AC的中点,连接OF并延长交
 于点D,过点D作⊙O的切线,交BA的延长线于点E.
于点D,过点D作⊙O的切线,交BA的延长线于点E.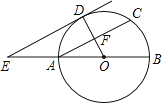
(1)求证:AC∥DE;
(2)连接CD,若OA=AE=a,写出求四边形ACDE面积的思路. -
科目: 来源: 题型:
查看答案和解析>>【题目】某高科技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A需要甲材料1.5kg,乙材料1kg,用5个工时;生产一件产品B需要甲材料0.5kg,乙材料0.3kg,用3个工时.生产一件产品A的利润为2100元,生产一件产品B的利润为900元.该企业现有甲材料150kg,乙材料90kg,求在不超过600个工时的条件下,生产产品A和产品B的利润之和的最大值(元).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知y是x的函数,自变量x的取值范围x>0,下表是y与x的几组对应值:
x
…
1
2
3
5
7
9
…
y
…
1.98
3.95
2.63
1.58
1.13
0.88
…
小腾根据学习函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.
下面是小腾的探究过程,请补充完整:
(1)如图,在平面直角坐标系xOy中,描出了以上表格中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(2)根据画出的函数图象,写出:
①x=4对应的函数值y约为
②该函数的一条性质: -
科目: 来源: 题型:
查看答案和解析>>【题目】某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为


(1)求频率分布直方图中
 的值;
的值;(2)估计该企业的职工对该部门评分不低于80的概率;
(3)从评分在
 的受访职工中,随机抽取2人,求此2人评分都在
的受访职工中,随机抽取2人,求此2人评分都在 的概率.
的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等比数列
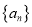 是递增数列,其前
是递增数列,其前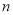 项和为
项和为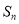 ,且
,且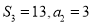 .
.(1)求数列
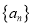 的通项公式;
的通项公式;(2)设
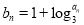 ,求数列
,求数列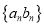 的前
的前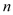 项和
项和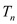 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某高科技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A需要甲材料1.5kg,乙材料1kg,用5个工时;生产一件产品B需要甲材料0.5kg,乙材料0.3kg,用3个工时.生产一件产品A的利润为2100元,生产一件产品B的利润为900元.该企业现有甲材料150kg,乙材料90kg,求在不超过600个工时的条件下,生产产品A和产品B的利润之和的最大值(元).
相关试题

