【题目】已知y是x的函数,自变量x的取值范围x>0,下表是y与x的几组对应值:
x | … | 1 | 2 | 3 | 5 | 7 | 9 | … |
y | … | 1.98 | 3.95 | 2.63 | 1.58 | 1.13 | 0.88 | … |
小腾根据学习函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.
下面是小腾的探究过程,请补充完整:
(1)如图,在平面直角坐标系xOy中,描出了以上表格中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(2)根据画出的函数图象,写出:
①x=4对应的函数值y约为
②该函数的一条性质:
参考答案:
【答案】
(1)
解:如图,

(2)2;该函数有最大值
【解析】解:①x=4对应的函数值y约为2;
②该函数有最大值.
故答案为2,该函数有最大值.
本题考查了函数的定义:对于函数概念的理解:①有两个变量;②一个变量的数值随着另一个变量的数值的变化而发生变化;③对于自变量的每一个确定的值,函数值有且只有一个值与之对应.
(1)按照自变量由小到大,利用平滑的曲线连结各点即可;
(2)①在所画的函数图象上找出自变量为4所对应的函数值即可;②利用函数图象有最高点求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了更好地规划进货的数量,保证蔬菜的新鲜程度,某蔬菜商店从某一年的销售数据中,随机抽取了8组数据作为研究对象,如下图所示(
 (吨)为买进蔬菜的质量,
(吨)为买进蔬菜的质量, 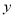 (天)为销售天数):
(天)为销售天数):
2
3
4
5
6
7
9
12
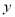
1
2
3
3
4
5
6
8
(Ⅰ)根据上表数据在下列网格中绘制散点图;

(Ⅱ)根据上表提供的数据,用最小二乘法求出
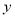 关于
关于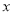 的线性回归方程
的线性回归方程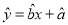 ;
;(Ⅲ)根据(Ⅱ)中的计算结果,若该蔬菜商店准备一次性买进25吨,则预计需要销售多少天.
参考公式:
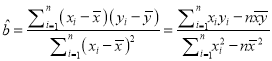 ,
, 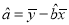 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,F为弦AC的中点,连接OF并延长交
 于点D,过点D作⊙O的切线,交BA的延长线于点E.
于点D,过点D作⊙O的切线,交BA的延长线于点E.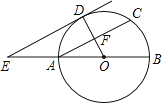
(1)求证:AC∥DE;
(2)连接CD,若OA=AE=a,写出求四边形ACDE面积的思路. -
科目: 来源: 题型:
查看答案和解析>>【题目】某高科技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A需要甲材料1.5kg,乙材料1kg,用5个工时;生产一件产品B需要甲材料0.5kg,乙材料0.3kg,用3个工时.生产一件产品A的利润为2100元,生产一件产品B的利润为900元.该企业现有甲材料150kg,乙材料90kg,求在不超过600个工时的条件下,生产产品A和产品B的利润之和的最大值(元).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
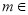 R,命题
R,命题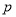 :对任意
:对任意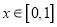 ,不等式
,不等式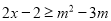 恒成立;命题
恒成立;命题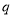 :存在
:存在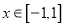 ,使得
,使得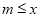 成立.
成立.(1)若
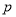 为真命题,求
为真命题,求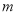 的取值范围;
的取值范围;(2)若
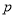 且
且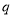 为假,
为假, 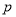 或
或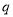 为真,求
为真,求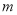 的取值范围;
的取值范围; -
科目: 来源: 题型:
查看答案和解析>>【题目】某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为


(1)求频率分布直方图中
 的值;
的值;(2)估计该企业的职工对该部门评分不低于80的概率;
(3)从评分在
 的受访职工中,随机抽取2人,求此2人评分都在
的受访职工中,随机抽取2人,求此2人评分都在 的概率.
的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等比数列
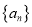 是递增数列,其前
是递增数列,其前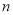 项和为
项和为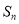 ,且
,且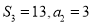 .
.(1)求数列
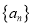 的通项公式;
的通项公式;(2)设
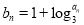 ,求数列
,求数列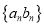 的前
的前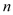 项和
项和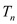 .
.
相关试题

