【题目】已知正三棱锥P﹣ABC底面边长为6,底边BC在平面α内,绕BC旋转该三棱锥,若某个时刻它在平面α上的正投影是等腰直角三角形,则此三棱锥高的取值范围是( ) 
A.(0, ![]() ]
]
B.(0, ![]() ]∪[
]∪[ ![]() ,3]
,3]
C.(0, ![]() ]
]
D.(0, ![]() ]∪[3,
]∪[3, ![]() ]
]
参考答案:
【答案】B
【解析】解:设正三棱锥P﹣ABC的高为h,
在△ABC中,设其中心为O,BC中点为E,则OE= ![]() ×
× ![]() ,
,
当h= ![]() 时,PE=
时,PE= ![]() ,PB=
,PB= ![]() =
= ![]() ,△PBC为等腰直角三角形,即当△PBC在平面α内时符合,
,△PBC为等腰直角三角形,即当△PBC在平面α内时符合,
P不在平面α内时,设p在α内的投影为P',PP'=d,∵△P'BC为等腰直角三角形,故P'E=3PE= ![]() >3,
>3,
又PE= ![]() =
= ![]() >3,
>3,
∴h2>6,∴h> ![]() .
.
由选项可知B符合,
故选:B.
【考点精析】关于本题考查的棱锥的结构特征,需要了解侧面、对角面都是三角形;平行于底面的截面与底面相似,其相似比等于顶点到截面距离与高的比的平方才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】【2017安徽淮北二模】选修4—4:坐标系与参数方程
在直角坐标系
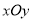 中, 以
中, 以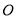 为极点,
为极点, 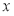 轴正半轴为极轴建立极坐标系, 圆
轴正半轴为极轴建立极坐标系, 圆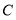 的极坐标方程为
的极坐标方程为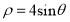 ,直线
,直线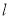 的参数方程为
的参数方程为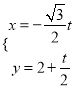 (t为参数), 直线
(t为参数), 直线 和圆
和圆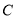 交于
交于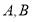 两点。
两点。(Ⅰ)求圆心的极坐标;
(Ⅱ)直线
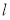 与
与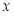 轴的交点为
轴的交点为 ,求
,求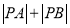 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
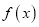 =ex(ex﹣a)﹣a2x.
=ex(ex﹣a)﹣a2x.(1)讨论
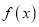 的单调性;
的单调性;(2)若
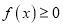 ,求a的取值范围.
,求a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设A,B为曲线C:y=
 上两点,A与B的横坐标之和为4.
上两点,A与B的横坐标之和为4.(1)求直线AB的斜率;
(2)设M为曲线C上一点,C在M处的切线与直线AB平行,且AM
 BM,求直线AB的方程.
BM,求直线AB的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
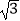 sinxcosx﹣sin2x+
sinxcosx﹣sin2x+  .
.
(1)求f(x)的最小正周期值;
(2)求f(x)的单调递增区间;
(3)求f(x)在[0, ]上的最值及取最值时x的值.
]上的最值及取最值时x的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前n项和为,且Sn=n2+n,
(1)求数列{an}的通项公式;
(2)令bn=3an , 求证:数列{bn}是等比数列. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司计划在今年内同时出售变频空调机和智能洗衣机,由于这两种产品的市场需求量非常大,有多少就能销售多少,因此该公司要根据实际情况(如资金、劳动力)确定产品的月供应量,以使得总利润达到最大.已知对这两种产品有直接限制的因素是资金和劳动力,通过调查,得到关于这两种产品的有关数据如表:
试问:怎样确定两种货物的月供应量,才能使总利润达到最大,最大利润是多少?资金
单位产品所需资金(百元)
空调机
洗衣机
月资金供应量(百元)
成本
30
20
300
劳动力(工资)
5
10
110
单位利润
6
8
相关试题

