【题目】设函数![]() (
(![]() 且
且![]() )是定义域为
)是定义域为![]() 的奇函数.
的奇函数.
(1)若![]() ,试求不等式
,试求不等式![]() 的解集;
的解集;
(2)若![]() ,且
,且![]() ,求
,求![]() 在
在![]() 上的最小值.
上的最小值.
参考答案:
【答案】(1)![]() 或
或![]() ;(2)当
;(2)当![]() 时,
时, ![]() 有最小值
有最小值![]() .
.
【解析】试题分析:由题意,先由奇函数的性质得出![]() 的值,(1)由
的值,(1)由![]() 求出
求出![]() 的范围,得出函数的单调性,利用单调性解不等式;(2)
的范围,得出函数的单调性,利用单调性解不等式;(2)![]() 得出
得出![]() 的值,将函数变为
的值,将函数变为![]()
![]() ,再利用换元法求出函数的最小值.
,再利用换元法求出函数的最小值.
试题解析:∵![]() 是定义域为
是定义域为![]() 的奇函数,∴
的奇函数,∴![]() ,∴
,∴![]() ,∴
,∴![]() .
.
(1)∵![]() ,∴
,∴![]() .又
.又![]() 且
且![]() ,∴
,∴![]() .∵
.∵![]() ,∴
,∴![]() .当
.当![]() 时,
时, ![]() 和
和![]() 在
在![]() 上均为增函数,∴
上均为增函数,∴![]() 在
在![]() 上为增函数.原不等式可化为
上为增函数.原不等式可化为![]() ,∴
,∴![]() ,即
,即![]() .∴
.∴![]() 或
或![]() .∴不等式的解集为
.∴不等式的解集为![]() 或
或![]() .
.
(2)∵![]() ,∴
,∴![]() ,即
,即![]() .∴
.∴![]() 或
或![]() (舍去).∴
(舍去).∴![]()
![]() .令
.令![]() (
(![]() ),则
),则![]() ,∵
,∵![]() 在
在![]() 上为增函数(由(1)可知),
上为增函数(由(1)可知),![]() ,即
,即![]() .
. ![]() ,
, ![]() .∴当
.∴当![]() 时,
时, ![]() 取得最小值2,即
取得最小值2,即![]() 取得最小值
取得最小值![]() ,此时
,此时![]() .故当
.故当![]() 时,
时, ![]() 有最小值
有最小值![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列函数中,是偶函数且在区间(0,+∞)上单调递减的函数是( )
A.y=2x
B.y=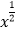
C.y=2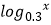
D.y=﹣x2 -
科目: 来源: 题型:
查看答案和解析>>【题目】若偶函数f(x)在(﹣∞,﹣1]上是增函数,则下列关系式中成立的是( )
A.f(﹣ )<f(﹣1)<f(2)
)<f(﹣1)<f(2)
B.f(﹣1)<f(﹣ )<f(2)
)<f(2)
C.f(2)<f(﹣1)<f(﹣ )
)
D.f(2)<f(﹣ )<f(﹣1)
)<f(﹣1) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x(lnx-ax)有两个极值点,则实数a的取值范围是( )
A. (-∞,0) B.
 C. (0,1) D. (0,+∞)
C. (0,1) D. (0,+∞) -
科目: 来源: 题型:
查看答案和解析>>【题目】某宾馆有相同标准的床位100张,根据经验,当该宾馆的床价(即每张床每天的租金)不超过10元时,床位可以全部租出,当床价高于10元时,每提高1元,将有3张床位空闲.为了获得较好的效益,该宾馆要给床位定一个合适的价格,条件是:①要方便结账,床价应为1元的整数倍;②该宾馆每日的费用支出为575元,床位出租的收入必须高于支出,而且高出得越多越好.若用x表示床价,用y表示该宾馆一天出租床位的净收入(即除去每日的费用支出后的收入).
(1)把y表示成x的函数,并求出其定义域;
(2)试确定该宾馆将床位定价为多少时,既符合上面的两个条件,又能使净收入最多?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知全集为实数集R,集合A={x|y=
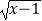 +
+ 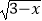 },B={x|log2x>1}.
},B={x|log2x>1}.
(1)分别求A∩B,(RB)∪A;
(2)已知集合C={x|1<x<a},若CA,求实数a的取值集合. -
科目: 来源: 题型:
查看答案和解析>>【题目】求函数f(x)=x2﹣2ax﹣1在[2,+∞)上的最小值.
相关试题

