【题目】如图,在三棱柱ABCA1B1C1中, CC1⊥平面ABC, AC⊥BC, AB1的中点为D,B1C∩BC1=E. 求证:
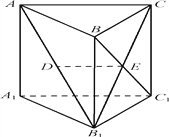
(1)DE∥平面AA1C1C;
(2)AC⊥平面BCC1B1.
参考答案:
【答案】(1)见解析;(2)见解析.
【解析】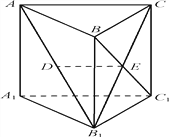
试题分析:(1)由三角形中位线定理得![]() ,由线面平行的判定定理可得
,由线面平行的判定定理可得![]() 平面
平面![]() ;(2)CC1⊥平面ABC可得AC⊥CC1,由已知AC⊥BC,从而由线面垂直的判定定理可得结果.
;(2)CC1⊥平面ABC可得AC⊥CC1,由已知AC⊥BC,从而由线面垂直的判定定理可得结果.
试题解析:(1) 由题意知,E为B1C的中点,又D为AB1的中点,因此DE∥AC.
因为DE![]() 平面AA1C1C,AC
平面AA1C1C,AC![]() 平面AA1C1C,所以DE∥平面AA1C1C.
平面AA1C1C,所以DE∥平面AA1C1C.
(2) CC1⊥平面ABC.
因为CC1⊥平面ABC,所以AC⊥CC1.
因为AC⊥BC,CC1![]() 平面BCC1B1,BC
平面BCC1B1,BC![]() 平面BCC1B1,
平面BCC1B1,
BC∩CC1=C,
所以AC⊥平面BCC1B1.
【方法点晴】本题主要考查线面平行的判定定理、线面垂直的判定定理,属于中档题.证明线面平行的常用方法:①利用线面平行的判定定理,使用这个定理的关键是设法在平面内找到一条与已知直线平行的直线,可利用几何体的特征,合理利用中位线定理、线面平行的性质或者构造平行四边形、寻找比例式证明两直线平行.②利用面面平行的性质,即两平面平行,在其中一平面内的直线平行于另一平面. 本题(1)是就是利用方法①证明的.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线C的标准方程是

(Ⅰ)求它的焦点坐标和准线方程;
(Ⅱ)直线
 过已知抛物线C的焦点且倾斜角为45°,且与抛物线的交点为A、B,求线段AB的长度.
过已知抛物线C的焦点且倾斜角为45°,且与抛物线的交点为A、B,求线段AB的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校高三年级在高校自主招生期间,把学生的平时成绩按“百分制”折算并排序,选出前300名学生,并对这300名学生按成绩分组,第一组
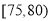 ,第二组
,第二组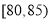 ,第三组
,第三组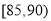 ,第四组
,第四组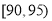 ,第五组
,第五组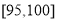 ,如图为频率分布直方图的一部分,其中第五组、第一组、第四组、第二组、第三组的人数依次成等差数列.
,如图为频率分布直方图的一部分,其中第五组、第一组、第四组、第二组、第三组的人数依次成等差数列.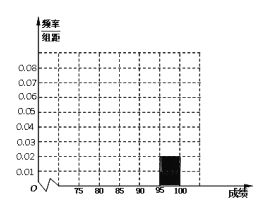
(I)请在图中补全频率直方图;
(II)若
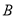 大学决定在成绩高的第4,5组中用分层抽样的方法抽取6名学生,并且分成2组,每组3人进行面试,求95分(包括95分)以上的同学被分在同一个小组的概率.
大学决定在成绩高的第4,5组中用分层抽样的方法抽取6名学生,并且分成2组,每组3人进行面试,求95分(包括95分)以上的同学被分在同一个小组的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
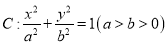 的左、右焦点分别为
的左、右焦点分别为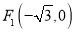 、
、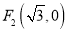 ,椭圆上的点
,椭圆上的点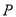 满足
满足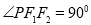 ,且
,且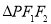 的面积为
的面积为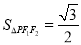 .
.(1)求椭圆
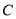 的方程;
的方程;(2)设椭圆
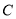 的左、右顶点分别为
的左、右顶点分别为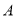 、
、 ,过点
,过点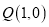 的动直线
的动直线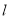 与椭圆
与椭圆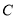 相交于
相交于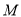 、
、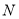 两点,直线
两点,直线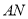 与直线
与直线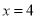 的交点为
的交点为 ,证明:点
,证明:点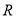 总在直线
总在直线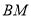 上.
上. -
科目: 来源: 题型:
查看答案和解析>>【题目】设数列
 的前
的前 项和为
项和为 ,点
,点 均在函数
均在函数 的图象上.
的图象上.(1)求证:数列
 为等差数列;
为等差数列;(2)设
 是数列
是数列 的前
的前 项和,求使
项和,求使 对所有
对所有 都成立的最小正整数
都成立的最小正整数 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
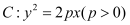 的焦点
的焦点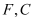 上一点
上一点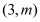 到焦点的距离为
到焦点的距离为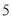 .
.(1)求
 的方程;
的方程;(2)过
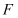 作直线
作直线 ,交
,交 于
于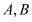 两点,若直线
两点,若直线 中点的纵坐标为
中点的纵坐标为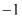 ,求直线
,求直线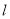 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
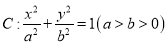 的左、右焦点分别为
的左、右焦点分别为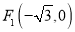 、
、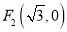 ,椭圆上的点
,椭圆上的点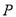 满足
满足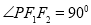 ,且
,且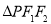 的面积为
的面积为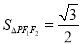 .
.(1)求椭圆
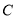 的方程;
的方程;(2)设椭圆
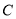 的左、右顶点分别为
的左、右顶点分别为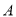 、
、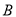 ,过点
,过点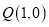 的动直线
的动直线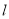 与椭圆
与椭圆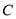 相交于
相交于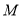 、
、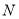 两点,直线
两点,直线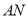 与直线
与直线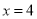 的交点为
的交点为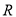 ,证明:点
,证明:点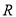 总在直线
总在直线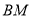 上.
上.
相关试题

