【题目】已知函数![]() (
(![]() )是偶函数.
)是偶函数.
(1)求![]() 的值;
的值;
(2)设![]() ,若函数
,若函数![]() 与
与![]() 的图象有且只有一个公共点,求实数
的图象有且只有一个公共点,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】
试题分析:(1)由![]() 可得
可得![]()
![]()
![]()
![]() ;(2)原命题转化为
;(2)原命题转化为![]()
![]() 只有一个解
只有一个解![]()
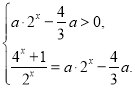 再利用换元思想和分类讨论思想解题.
再利用换元思想和分类讨论思想解题.
试题解析:(1)∵函数![]() (
(![]() )是偶函数,
)是偶函数,
∴![]()
![]() 恒成立,
恒成立,
∴![]() ,则
,则![]() .
.
(2)![]() ,函数
,函数![]() 与
与![]() 的图象有且只有一个公共点,即方程
的图象有且只有一个公共点,即方程![]() 只有一个解,由已知得
只有一个解,由已知得![]() ,
,
∴![]() 方程等价于
方程等价于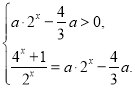
设![]() (
(![]() ),则有关于
),则有关于![]() 的方程
的方程![]() ,
,
若![]() ,即
,即![]() ,则需关于
,则需关于![]() 的方程
的方程![]() 只有一个大于
只有一个大于![]() 正数解,
正数解,
设![]() ,∵
,∵![]() ,
,![]() ,
,
∴恰好有一个大于![]() 的正解,
的正解,
∴![]() 满足题意;
满足题意;
若![]() ,即
,即![]() 时,解得
时,解得![]() ,不满足题意;
,不满足题意;
若![]() ,即
,即![]() 时,由
时,由![]() ,得
,得![]() 或
或![]() ,
,
当![]() 时,则需关于
时,则需关于![]() 的方程
的方程![]() 只有一个小于
只有一个小于![]() 的整数解.
的整数解.
解得![]() 满足题意;当
满足题意;当![]() 时,
时,![]() 不满足题意.
不满足题意.
综上所述,实数![]() 的取值范围是
的取值范围是![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某城市
 户居民的月平均用电量(单位:度),以
户居民的月平均用电量(单位:度),以 ,
, ,
, ,
, ,
, ,
, ,
, 分组的频率分布直方图如图.
分组的频率分布直方图如图.
(I)求直方图中
 的值;
的值; (II)求月平均用电量的众数和中位数;
(III)在月平均用电量为
 ,
, ,
, ,
, 的四组用户中,用分层抽样的方法抽取
的四组用户中,用分层抽样的方法抽取 户居民,则月平均用电量在
户居民,则月平均用电量在 的用户中应抽取多少户?
的用户中应抽取多少户? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知四棱锥
 ,底面
,底面 是
是 、边长为
、边长为 的菱形,又
的菱形,又 底
底 ,且
,且 ,点
,点 分别是棱
分别是棱 的中点.
的中点.
(1)证明:
 平面
平面 ;
;(2)证明:平面
 平面
平面 ;
;(3)求点
 到平面
到平面 的距离.[
的距离.[ -
科目: 来源: 题型:
查看答案和解析>>【题目】正方体
 的棱长为1,
的棱长为1,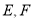 分别是棱
分别是棱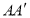 ,
, 的中点,过直线
的中点,过直线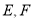 的平面分别与棱
的平面分别与棱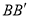 、
、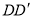 交于
交于 ,设
,设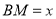 ,
,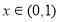 ,给出以下四个命题:
,给出以下四个命题:①四边形
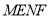 为平行四边形;
为平行四边形;②若四边形
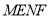 面积
面积 ,
,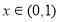 ,则
,则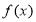 有最小值;
有最小值;③若四棱锥
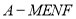 的体积
的体积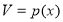
 ,
,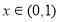 ,则
,则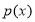 为常函数;
为常函数;④若多面体
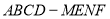 的体积
的体积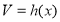 ,
,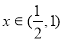 ,则
,则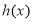 为单调函数.
为单调函数.其中假命题为( )
A.① ③ B.② C.③④ D.④
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某地参加2015 年夏令营的
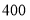 名学生的身体健康情况,将学生编号为
名学生的身体健康情况,将学生编号为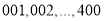 ,采用系统抽样的方法抽取一个容量为
,采用系统抽样的方法抽取一个容量为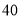 的样本,且抽到的最小号码为
的样本,且抽到的最小号码为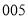 ,已知这
,已知这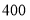 名学生分住在三个营区,从
名学生分住在三个营区,从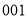 到
到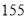 在第一营区,从
在第一营区,从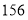 到
到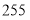 在第二营区,从
在第二营区,从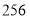 到
到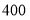 在第三营区,则第一、第二、第三营区被抽中的人数分别为( )
在第三营区,则第一、第二、第三营区被抽中的人数分别为( )A.
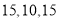 B.
B.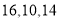
C.
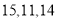 D.
D.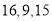
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (
( ),其最小正周期为
),其最小正周期为 .
.(1)求
 在区间
在区间 上的减区间;
上的减区间;(2)将函数
 图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得的图象向右平移
图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得的图象向右平移 个单位,得到函数
个单位,得到函数 的图象,若关于
的图象,若关于 的方程
的方程 在区间
在区间 上有且只有一个实数根,求实数
上有且只有一个实数根,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在梯形
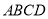 中,
中, 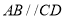 ,
, 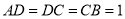 ,
, 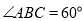 ,四边形
,四边形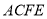 为矩形,平面
为矩形,平面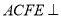 平面
平面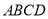 ,
, 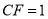 .
.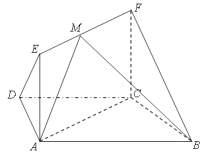
(1)求证:
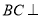 平面
平面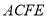 ;
;(2)点
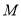 在线段
在线段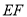 上运动,设平面
上运动,设平面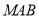 与平面
与平面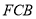 所成二面角的平面角为
所成二面角的平面角为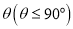 ,试求
,试求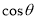 的取值范围.
的取值范围.
相关试题

