【题目】下面给出了四个类比推理:
(1)由“若![]() 则
则![]() ”类比推出“若
”类比推出“若![]() 为三个向量则
为三个向量则![]() ”;
”;
(2)“a,b为实数,![]() 则a=b=0”类比推出“
则a=b=0”类比推出“![]() 为复数,若
为复数,若![]() ”
”
(3)“在平面内,三角形的两边之和大于第三边”类比推出“在空间中,四面体的任意三个面的面积之和大于第四个面的面积”
(4)“在平面内,过不在同一条直线上的三个点有且只有一个圆”类比推出“在空间中,过不在同一个平面上的四个点有且只有一个球”.
上述四个推理中,结论正确的个数有( )
A.1个 B.2个 C.3个 D.4个
参考答案:
【答案】B
【解析】
试题分析:容易验证结论是错误的.事实上,若三个向量都是单位向量,其夹角不同则(1)不成立;若取![]() ,显然满足题设,即(2)不成立.其中(3)(4)是正确的证明过程略.故应选B.
,显然满足题设,即(2)不成立.其中(3)(4)是正确的证明过程略.故应选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
 是两条不同的直线,
是两条不同的直线,  是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题: ①若
 ,则
,则 ②若
②若 ,则
,则
③若
 ,则
,则 ④若
④若 ,则
,则
其中正确命题的序号是( )
A. ①和② B. ②和③ C. ③和④ D. ①和④
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某地区某种农产品的年产量
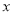 (单位:吨)对价格
(单位:吨)对价格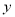 (单位:千元/吨)和利润
(单位:千元/吨)和利润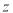 的影响,对近五年该农产品的年产量和价格统计如下表:
的影响,对近五年该农产品的年产量和价格统计如下表:
(1)求
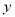 关于
关于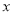 的线性回归方程;
的线性回归方程;(2)若每吨该农产品的成本为2千元,假设该农产品可全部卖出,预测当年产量为多少时,年利润
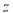 取到最大值?(结果保留两位小数)
取到最大值?(结果保留两位小数)参考公式:
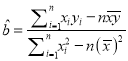 ,
, 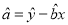
参考数据:
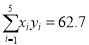 ,
, 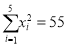 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】设
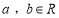 ,函数
,函数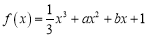 ,
,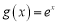 (
( 为自然对数的底数),且函数
为自然对数的底数),且函数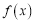 的图象与函数
的图象与函数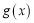 的图象在
的图象在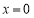 处有公共的切线.
处有公共的切线.(Ⅰ)求
 的值;
的值;(Ⅱ)讨论函数
 的单调性;
的单调性;(Ⅲ)证明:当
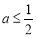 时,
时, 在区间
在区间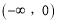 内恒成立.
内恒成立. -
科目: 来源: 题型:
查看答案和解析>>【题目】共享单车是指由企业在校园、公交站点、商业区、公共服务区等场所提供的自行车单车共享服务,由于其依托“互联网+”,符合“低碳出行”的理念,已越来越多地引起了人们的关注.某部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照[50,60),[60,70),…,[90,100] 分成5组,制成如图所示频率分直方图.
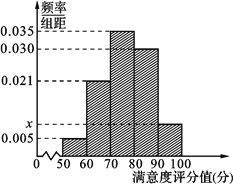
(1) 求图中
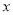 的值;
的值;(2) 已知满意度评分值在[90,100]内的男生数与女生数的比为2:1,若在满意度评分值为[90,100]的人中随机抽取4人进行座谈,设其中的女生人数为随机变量
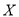 ,求
,求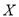 的分布列和数学期望.
的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
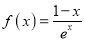 .
.(1)求曲线
 在点
在点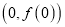 处的切线方程和函数
处的切线方程和函数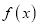 的极值:
的极值:(2)若对任意
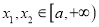 ,都有
,都有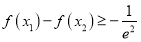 成立,求实数
成立,求实数 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
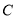 过点
过点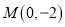 和点
和点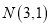 ,且圆心
,且圆心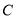 在直线
在直线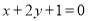 上.
上.(1)求圆
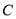 的方程;
的方程;(2)过点
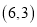 作圆
作圆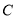 的切线,求切线方程.
的切线,求切线方程.(3)设直线
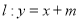 ,且直线
,且直线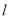 被圆
被圆 所截得的弦为
所截得的弦为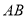 ,满足
,满足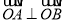 ,求直线
,求直线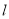 的方程.
的方程.
相关试题

