【题目】已知圆![]() 过点
过点![]() 和点
和点![]() ,且圆心
,且圆心![]() 在直线
在直线![]() 上.
上.
(1)求圆![]() 的方程;
的方程;
(2)过点![]() 作圆
作圆![]() 的切线,求切线方程.
的切线,求切线方程.
(3)设直线![]() ,且直线
,且直线![]() 被圆
被圆![]() 所截得的弦为
所截得的弦为![]() ,满足
,满足![]() ,求直线
,求直线![]() 的方程.
的方程.
参考答案:
【答案】(1) x2+y2-6x+4y+4=0. (2) ![]() 或
或![]() .(3)y=x-1或y=x-4.
.(3)y=x-1或y=x-4.
【解析】试题分析:(1)设圆心C(a,b),由两点间距离公式及圆心在直线上,列出方程组,求出圆心坐标,进而求出圆半径,由此能求出圆C的方程.
(2)当切线的斜率k存在时,设过点(6,3)的切线方程为kx﹣y﹣6k+3=0,则圆心C(3,﹣2)到切线的距离d=![]() ,求出k,从而求出切线方程;当切线斜率k不存在时,切线方程为x=6,成立.由此能求出切线方程.
,求出k,从而求出切线方程;当切线斜率k不存在时,切线方程为x=6,成立.由此能求出切线方程.
(3)由题意得OA⊥OB,从而|OA|2+|OB|2=|AB|2,进而解得m=-1或m=-4,由此能求出直线l的方程.
试题解析:
(Ⅰ)设圆C的方程为x2+y2+Dx+Ey+F=0,
则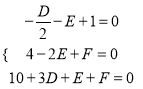 ,解得D=-6,E=4,F=4,
,解得D=-6,E=4,F=4,
所以圆C的方程为x2+y2-6x+4y+4=0.
(Ⅱ)圆C的方程为![]() ,
,
当斜率存在时,设切线方程为![]() ,则
,则
![]() ,解得
,解得![]() ,
,
所以切线方程为![]() ,即
,即![]() .
.
当斜率不存在时, ![]() .
.
所以所求的切线方程为![]() 或
或![]() .
.
(Ⅲ)直线l的方程为y=x+m.
设A(x1,y1),B(x2,y2),
则联立![]() 消去y得2x2+2(m-1)x+m2+4m+4=0,(*)
消去y得2x2+2(m-1)x+m2+4m+4=0,(*)
∴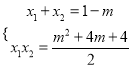 ∴y1y2=(x1+m)(x2+m)=x1x2+m
∴y1y2=(x1+m)(x2+m)=x1x2+m
∵∠AOB=90°,∴|OA|2+|OB|2=|AB|2,
∴![]() =(x1-x2)2+(y1-y2)2,
=(x1-x2)2+(y1-y2)2,
得x1x2+y1y2=0,∴2x1x2+m(x1+x2)+m2=0,
即m2+4m+4+m(1-m)+m2=0,解得m=-1或m=-4.
容易验证m=-1或m=-4时方程(*)有实根.
所以直线l的方程是y=x-1或y=x-4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面给出了四个类比推理:
(1)由“若
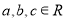 则
则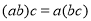 ”类比推出“若
”类比推出“若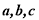 为三个向量则
为三个向量则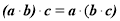 ”;
”;(2)“a,b为实数,
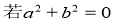 则a=b=0”类比推出“
则a=b=0”类比推出“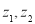 为复数,若
为复数,若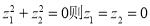 ”
”(3)“在平面内,三角形的两边之和大于第三边”类比推出“在空间中,四面体的任意三个面的面积之和大于第四个面的面积”
(4)“在平面内,过不在同一条直线上的三个点有且只有一个圆”类比推出“在空间中,过不在同一个平面上的四个点有且只有一个球”.
上述四个推理中,结论正确的个数有( )
A.1个 B.2个 C.3个 D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】共享单车是指由企业在校园、公交站点、商业区、公共服务区等场所提供的自行车单车共享服务,由于其依托“互联网+”,符合“低碳出行”的理念,已越来越多地引起了人们的关注.某部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照[50,60),[60,70),…,[90,100] 分成5组,制成如图所示频率分直方图.
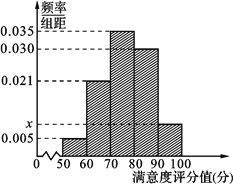
(1) 求图中
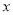 的值;
的值;(2) 已知满意度评分值在[90,100]内的男生数与女生数的比为2:1,若在满意度评分值为[90,100]的人中随机抽取4人进行座谈,设其中的女生人数为随机变量
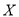 ,求
,求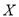 的分布列和数学期望.
的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
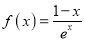 .
.(1)求曲线
 在点
在点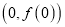 处的切线方程和函数
处的切线方程和函数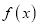 的极值:
的极值:(2)若对任意
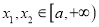 ,都有
,都有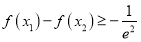 成立,求实数
成立,求实数 的最小值.
的最小值. -
科目: 来源: 题型:
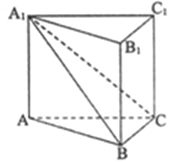
查看答案和解析>>【题目】如图,在直三棱柱
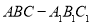 中,平面
中,平面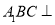 侧面
侧面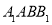 ,且
,且 .
.
(1)求证:
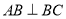 ;
;(2)若直线
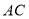 与平面
与平面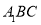 所成角的大小为
所成角的大小为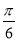 ,求锐二面角
,求锐二面角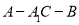 的大小.
的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】设甲、乙、丙三个乒乓球协会的运动员人数分别为27,9,18,先采用分层抽样的方法从这三个协会中抽取6名运动员参加比赛.
(Ⅰ)求应从这三个协会中分别抽取的运动员人数;
(Ⅱ)将抽取的6名运动员进行编号,编号分别为
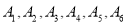 ,从这6名运动员中随机抽取2名参加双打比赛.
,从这6名运动员中随机抽取2名参加双打比赛.(ⅰ)用所给编号列出所有可能的结果;
(ⅱ)设
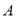 为事件“编号为
为事件“编号为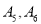 的两名运动员至少有一人被抽到”,求事件
的两名运动员至少有一人被抽到”,求事件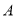 发生的概率.
发生的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
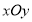 中,已知曲线
中,已知曲线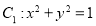 ,以平面直角坐标系
,以平面直角坐标系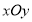 的原点
的原点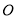 为极点,
为极点,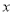 轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线
轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线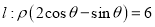 .
.(1)将曲线
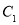 上的所有点的横坐标、纵坐标分别伸长为原来的
上的所有点的横坐标、纵坐标分别伸长为原来的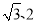 倍后得到曲线
倍后得到曲线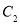 .试写出直线
.试写出直线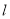 的直角坐标方程和曲线
的直角坐标方程和曲线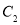 的参数方程:
的参数方程:(2)在曲线
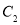 上求一点
上求一点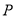 ,使点
,使点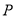 到直线
到直线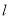 的距离最大,并求出此最大值.
的距离最大,并求出此最大值.
相关试题

