【题目】如图,在直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 中点,
中点,![]() 与
与![]() 交于点
交于点![]() .
.
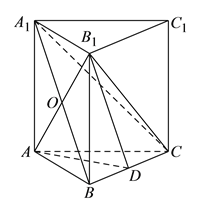
(1)求证:![]() 平面
平面![]() ;
;
(2)求证:![]() 平面
平面![]() ;
;
(3)求三棱锥![]() 的表面积.
的表面积.
参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】试题分析:(1)证明:连结![]() ,可得
,可得![]() 为
为![]() 的中位线,可得
的中位线,可得![]() ,根据线面平行的判定定理可得
,根据线面平行的判定定理可得![]() 平面
平面![]() ;(2)在直三棱柱
;(2)在直三棱柱![]() 中,可证
中,可证![]() 平面
平面![]() ,从而可得
,从而可得![]() ,又
,又![]() ,
,![]() ,即可证明
,即可证明![]() 平面
平面![]() ;(3)
;(3)![]() ,分别利用三角形面积公式求出各三角形面积,求和即可得结果.
,分别利用三角形面积公式求出各三角形面积,求和即可得结果.
试题解析:(1)证明:连结![]() ,
,
∵直三棱柱![]() ,
,![]() ,
,
∴四边形![]() 为正方形,
为正方形,
∴![]() 为
为![]() 中点,
中点,
∵![]() 为
为![]() 中点,
中点,
∴![]() ,
,
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(2)证明:方法1,∵直三棱柱![]() ,
,
∴![]() ,
,
又∵![]() ,
,![]() ,
,
∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,
,
∴![]() ,
,
∵正方形![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() 平面
平面![]() .
.
方法2:∵直三棱柱![]() ,
,
∴平面![]() 平面
平面![]() ,
,
∵平面![]() 平面
平面![]() ,
,![]() ,
,
∵![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,
,
∴![]() ,
,
∵正方形![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() 平面
平面![]() .
.
(3)![]()
![]()
![]() .
.
【方法点晴】本题主要考查线面平行的判定定理、线面垂直的判定定理、利用等积变换求三棱锥体积,属于难题.证明线面平行的常用方法:①利用线面平行的判定定理,使用这个定理的关键是设法在平面内找到一条与已知直线平行的直线,可利用几何体的特征,合理利用中位线定理、线面平行的性质或者构造平行四边形、寻找比例式证明两直线平行.②利用面面平行的性质,即两平面平行,在其中一平面内的直线平行于另一平面. 本题(1)是就是利用方法①证明的.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司为了解广告投入对销售收益的影响,在若干地区各投入
 万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从
万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从 开始计数的. [附:回归直线的斜率和截距的最小二乘估计公式分别为.]
开始计数的. [附:回归直线的斜率和截距的最小二乘估计公式分别为.](1)根据频率分布直方图计算图中各小长方形的宽度;
(2)试估计该公司投入
 万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);
万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);(3)该公司按照类似的研究方法,测得另外一些数据,并整理得到下表:
广告投入
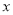 (单位:万元)
(单位:万元)1
2
3
4
5
销售收益
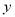 (单位:万元)
(单位:万元)2
3
2
7
由表中的数据显示,
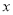 与
与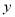 之间存在着线性相关关系,请将(2)的结果填入空白栏,并求出
之间存在着线性相关关系,请将(2)的结果填入空白栏,并求出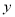 关于
关于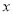 的回归直线方程.
的回归直线方程.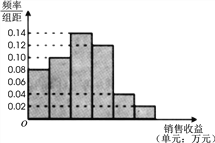
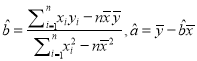
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
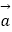 =(sinx,cosx),
=(sinx,cosx), 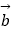 =(sin(x﹣
=(sin(x﹣  ),sinx),函数f(x)=2
),sinx),函数f(x)=2 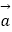
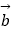 ,g(x)=f(
,g(x)=f( 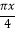 ).
).
(1)求f(x)在[ ,π]上的最值,并求出相应的x的值;
,π]上的最值,并求出相应的x的值;
(2)计算g(1)+g(2)+g(3)+…+g(2014)的值;
(3)已知t∈R,讨论g(x)在[t,t+2]上零点的个数. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=x3+2x2﹣4x+5在[﹣4,1]上的最大值和最小值分别是( )
A.13,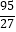
B.4,﹣11
C.13,﹣11
D.13,最小值不确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
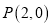 ,⊙
,⊙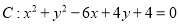 .
.(Ⅰ)当直线
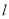 过点
过点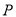 且与圆心
且与圆心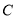 的距离为
的距离为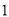 时,求直线
时,求直线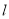 的方程.
的方程.(Ⅱ)设过点
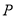 的直线与⊙
的直线与⊙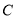 交于
交于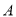 ,
, 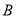 两点,且
两点,且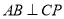 ,求以线段
,求以线段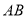 为直径的圆的方程.
为直径的圆的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知定点
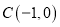 及椭圆
及椭圆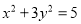 ,过点
,过点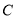 的动直线与椭圆相交于
的动直线与椭圆相交于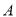 ,
,  两点.
两点.(1)若线段
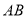 中点的横坐标是
中点的横坐标是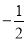 ,求直线
,求直线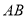 的方程;
的方程;(2)设点
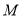 的坐标为
的坐标为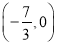 ,求证:
,求证: 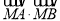 为定值.
为定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分13分)
已知椭圆
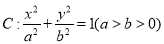 的短轴长为
的短轴长为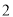 ,且与抛物线
,且与抛物线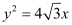 有共同的焦点,椭圆
有共同的焦点,椭圆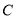 的左顶点为A,右顶点为
的左顶点为A,右顶点为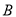 ,点
,点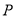 是椭圆
是椭圆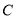 上位于
上位于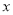 轴上方的动点,直线
轴上方的动点,直线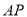 ,
,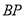 与直线
与直线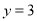 分别交于
分别交于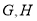 两点.
两点.(I)求椭圆
 的方程;
的方程;(Ⅱ)求线段
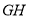 的长度的最小值;
的长度的最小值;(Ⅲ)在线段
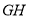 的长度取得最小值时,椭圆
的长度取得最小值时,椭圆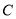 上是否存在一点
上是否存在一点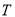 ,使得
,使得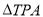 的面积为
的面积为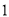 ,若存在求出点
,若存在求出点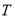 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
相关试题

