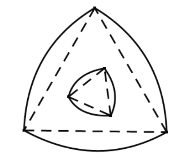
【题目】勒洛三角形是具有类似圆的“定宽性”的曲线,它是由德国机械工程专家、机构运动学家勒洛首先发现,其作法是:以等边三角形每个顶点为圆心,以边长为半径,在另两个顶点间作一段弧,三段弧围成的曲边三角形就是勒洛三角形.如图中的两个勒洛三角形,它们所对应的等边三角形的边长比为![]() ,若从大的勒洛三角形中随机取一点,则此点取自小勒洛三角形内的概率为( )
,若从大的勒洛三角形中随机取一点,则此点取自小勒洛三角形内的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
参考答案:
【答案】A
【解析】
先求出各自的面积,根据面积比即可求出结果.
解:设图中的小的勒洛三角形所对应的等边三角形的边长为![]() ,
,
则小勒洛三角形的面积![]() ,
,
因为大小两个勒洛三角形,它们所对应的等边三角形的边长比为![]() ,
,
所以大勒洛三角形的面积![]() ,
,
若从大的勒洛三角形中随机取一点,则此点取自小勒洛三角形内的概率![]() .
.
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一块各面均涂有油漆的正方体被锯成27个大小相同的小正方体,若将这些小正方体均匀地搅混在一起,从中任意取出一个,则取出的小正方体两面涂有油漆的概率是( )
A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】半正多面体(semiregular solid)亦称“阿基米德多面体”,如图所示,是由边数不全相同的正多边形为面的多面体,体现了数学的对称美.将正方体沿交于一顶点的三条棱的中点截去一个三棱锥,如此共可截去八个三棱锥,得到一个有十四个面的半正多面体,它们的边长都相等,其中八个为正三角形,六个为正方形,称这样的半正多面体为二十四等边体.若二十四等边体的棱长为
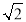 ,则该二十四等边体外接球的表面积为( )
,则该二十四等边体外接球的表面积为( )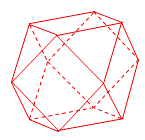
A.
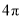 B.
B.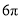 C.
C.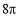 D.
D.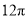
-
科目: 来源: 题型:
查看答案和解析>>【题目】某汽车站每天均有3辆开往省城的分为上、中、下等级的客车,某天袁先生准备在该汽车站乘车前往省城办事,但他不知道客车的车况,也不知道发车顺序.为了尽可能乘上上等车,他采取如下策略:先放过一辆,如果第二辆比第一辆好则上第二辆,否则上第三辆.则他乘上上等车的概率为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,椭圆
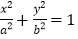
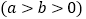 的左焦点为
的左焦点为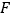 ,右顶点为
,右顶点为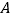 ,上顶点为
,上顶点为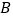 .
.(1)已知椭圆的离心率为
 ,线段
,线段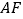 中点的横坐标为
中点的横坐标为 ,求椭圆的标准方程;
,求椭圆的标准方程;(2)已知△
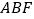 外接圆的圆心在直线
外接圆的圆心在直线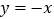 上,求椭圆的离心率
上,求椭圆的离心率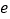 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A,B是抛物线C:y2=4x上两点,线段AB的垂直平分线与x轴有唯一的交点P(x0,0).
(1)求证:x0>2;
(2)若直线AB过抛物线C的焦点F,且|AB|=10,求|PF|.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业为确定下一年度投入某种产品的生产所需的资金,需了解每投入2千万资金后,工人人数
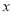 (单位:百人)对年产能
(单位:百人)对年产能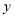 (单位:千万元)的影响,对投入的人力和年产能的数据作了初步处理,得到散点图和统计量表.
(单位:千万元)的影响,对投入的人力和年产能的数据作了初步处理,得到散点图和统计量表.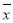
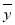
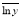
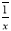
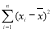
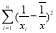
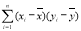
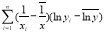
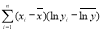
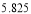
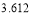
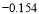
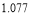
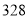

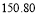
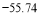
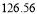
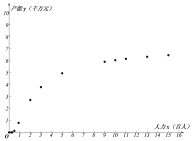
(1)根据散点图判断:
 与
与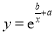 哪一个适宜作为年产能
哪一个适宜作为年产能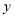 关于投入的人力
关于投入的人力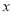 的回归方程类型?并说明理由?
的回归方程类型?并说明理由?(2)根据(1)的判断结果及相关的计算数据,建立
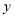 关于
关于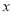 的回归方程;
的回归方程;(3)现该企业共有2000名生产工人,资金非常充足,为了使得年产能达到最大值,则下一年度共需投入多少资金(单位:千万元)?
附注:对于一组数据
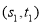 ,
,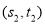 ,…,
,…,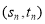 ,其回归直线
,其回归直线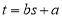 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为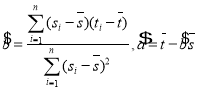 ,(说明:
,(说明: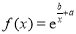 的导函数为
的导函数为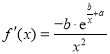 )
)
相关试题

