【题目】某企业为确定下一年度投入某种产品的生产所需的资金,需了解每投入2千万资金后,工人人数![]() (单位:百人)对年产能
(单位:百人)对年产能![]() (单位:千万元)的影响,对投入的人力和年产能的数据作了初步处理,得到散点图和统计量表.
(单位:千万元)的影响,对投入的人力和年产能的数据作了初步处理,得到散点图和统计量表.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
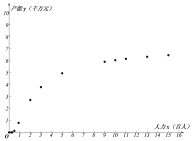
(1)根据散点图判断:![]() 与
与![]() 哪一个适宜作为年产能
哪一个适宜作为年产能![]() 关于投入的人力
关于投入的人力![]() 的回归方程类型?并说明理由?
的回归方程类型?并说明理由?
(2)根据(1)的判断结果及相关的计算数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)现该企业共有2000名生产工人,资金非常充足,为了使得年产能达到最大值,则下一年度共需投入多少资金(单位:千万元)?
附注:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为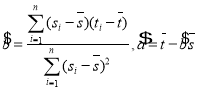 ,(说明:
,(说明:![]() 的导函数为
的导函数为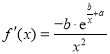 )
)
参考答案:
【答案】(1)选择![]() ,理由见解析;(2)
,理由见解析;(2)![]() ;(3)20千万
;(3)20千万
【解析】
(1)由图可知![]() 适宜作为年产能
适宜作为年产能![]() 关于投入的人力
关于投入的人力![]() 的回归方程类型;
的回归方程类型;
(2)由![]() ,得
,得![]() ,再利用最小二乘法求出
,再利用最小二乘法求出![]() ,从而得到
,从而得到![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)利用导数求得当![]() 时,
时,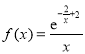 取得最大值.
取得最大值.
(1)由图可知![]() 适宜作为年产能
适宜作为年产能![]() 关于投入的人力
关于投入的人力![]() 的回归方程类型
的回归方程类型
![]() 若选择
若选择![]() ,则
,则![]() ,此时当
,此时当![]() 接近于0时,
接近于0时,![]() 必小于0,
必小于0,
故选择![]() 作为年产能
作为年产能![]() 关于投入的人力
关于投入的人力![]() 的回归方程类型
的回归方程类型
(2)由![]() ,得
,得![]() ,故
,故![]() 与
与![]() 符合线性回归,
符合线性回归,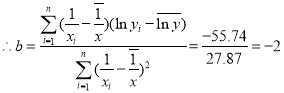 .
.
![]() ,
,
![]() ,即
,即![]() ,
,
![]() 关于
关于![]() 的回归方程
的回归方程![]() .
.
(3)当人均产能达到最大时,年产能也达到最大,
由(2)可知人均产能函数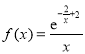 ,
,
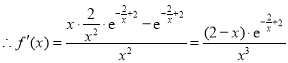 ,
,
![]() 时,
时,![]() ,
,![]() 时
时![]() ,
,
![]() 时,
时,![]() 单调递增,
单调递增,![]() 时,
时,![]() 单调递减,
单调递减,
![]() 当
当![]() 时,人均产能函数
时,人均产能函数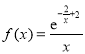 达到最大值,
达到最大值,
因此,每2千万资金安排2百人进行生产,能使人均产能达到最大,
![]() 对于该企业共有2000名生产工人,且资金充足,
对于该企业共有2000名生产工人,且资金充足,
![]() 下一年度应该投入20千万资金进行生产,可以适当企业的产能达到最大.
下一年度应该投入20千万资金进行生产,可以适当企业的产能达到最大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】勒洛三角形是具有类似圆的“定宽性”的曲线,它是由德国机械工程专家、机构运动学家勒洛首先发现,其作法是:以等边三角形每个顶点为圆心,以边长为半径,在另两个顶点间作一段弧,三段弧围成的曲边三角形就是勒洛三角形.如图中的两个勒洛三角形,它们所对应的等边三角形的边长比为
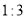 ,若从大的勒洛三角形中随机取一点,则此点取自小勒洛三角形内的概率为( )
,若从大的勒洛三角形中随机取一点,则此点取自小勒洛三角形内的概率为( )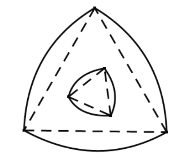
A.
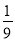 B.
B.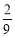 C.
C.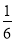 D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,椭圆
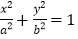
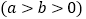 的左焦点为
的左焦点为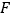 ,右顶点为
,右顶点为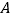 ,上顶点为
,上顶点为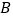 .
.(1)已知椭圆的离心率为
 ,线段
,线段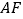 中点的横坐标为
中点的横坐标为 ,求椭圆的标准方程;
,求椭圆的标准方程;(2)已知△
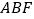 外接圆的圆心在直线
外接圆的圆心在直线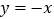 上,求椭圆的离心率
上,求椭圆的离心率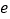 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A,B是抛物线C:y2=4x上两点,线段AB的垂直平分线与x轴有唯一的交点P(x0,0).
(1)求证:x0>2;
(2)若直线AB过抛物线C的焦点F,且|AB|=10,求|PF|.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某科研课题组通过一款手机APP软件,调查了某市1000名跑步爱好者平均每周的跑步量(简称“周跑量”),得到如下的频数分布表
周跑量(km/周)









人数
100
120
130
180
220
150
60
30
10
(1)在答题卡上补全该市1000名跑步爱好者周跑量的频率分布直方图:

注:请先用铅笔画,确定后再用黑色水笔描黑
(2)根据以上图表数据计算得样本的平均数为
 ,试求样本的中位数(保留一位小数),并用平均数、中位数等数字特征估计该市跑步爱好者周跑量的分布特点
,试求样本的中位数(保留一位小数),并用平均数、中位数等数字特征估计该市跑步爱好者周跑量的分布特点(3)根据跑步爱好者的周跑量,将跑步爱好者分成以下三类,不同类别的跑者购买的装备的价格不一样,如下表:
周跑量
小于20公里
20公里到40公里
不小于40公里
类别
休闲跑者
核心跑者
精英跑者
装备价格(单位:元)
2500
4000
4500
根据以上数据,估计该市每位跑步爱好者购买装备,平均需要花费多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】求下列椭圆的标准方程:
(1)焦点在
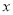 轴上,离心率
轴上,离心率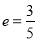 ,且经过点
,且经过点 ;
;(2)以坐标轴为对称轴,且长轴长是短轴长的
 倍,并且过点
倍,并且过点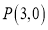 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系
 中,曲线
中,曲线 的参数方程为
的参数方程为 (
(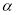 为参数).以
为参数).以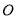 为极点,
为极点,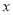 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线 的极坐标方程为
的极坐标方程为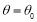 (
(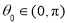 ),将曲线
),将曲线 向左平移2个单位长度得到曲线
向左平移2个单位长度得到曲线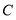 .
.(1)求曲线
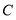 的普通方程和极坐标方程;
的普通方程和极坐标方程;(2)设直线
 与曲线
与曲线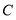 交于
交于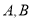 两点,求
两点,求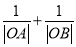 的取值范围.
的取值范围.
相关试题

