【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,短轴长为2.
,短轴长为2.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,
两点, ![]() 为坐标原点,若
为坐标原点,若![]() ,求原点
,求原点![]() 到直线
到直线![]() 的距离的取值范围.
的距离的取值范围.
参考答案:
【答案】(1)![]() ;(2)
;(2)
【解析】试题分析:(1)由已知求得![]() ,再由椭圆离心率及隐含条件求得
,再由椭圆离心率及隐含条件求得![]() ,则椭圆方程可求;(2)联立直线方程与椭圆方程,化为关于x的一元二次方程,由判别式大于0求得
,则椭圆方程可求;(2)联立直线方程与椭圆方程,化为关于x的一元二次方程,由判别式大于0求得![]() ,再由
,再由![]() ,可得
,可得![]() ,从而求得
,从而求得![]() 的范围,再由点到直线的距离公式求出原点
的范围,再由点到直线的距离公式求出原点![]() 到直线
到直线![]() 的距离,则取值范围可求.
的距离,则取值范围可求.
试题解析:(1)设焦距为![]() ,由已知
,由已知![]() ,
, ![]() ,∴
,∴![]() ,又
,又![]() ,解得
,解得![]() ,∴椭圆
,∴椭圆![]() 的标准方程为
的标准方程为![]() ;
;
(2)设![]() ,
, ![]() ,联立
,联立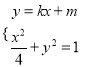 得
得![]() ,依题意,
,依题意, ![]() ,化简得
,化简得![]() ,①,
,①, ![]() ,
, ![]() ,
, ![]() ,若
,若![]() ,则
,则![]() ,即
,即![]() ,∴
,∴![]() ,∴
,∴ ,即
,即![]() ,化简得
,化简得![]() ,②,由①②得
,②,由①②得![]() ,
, ![]() ,∵原点
,∵原点![]() 到直线
到直线![]() 的距离
的距离![]() ,∴
,∴ ,又∵
,又∵![]() ,∴
,∴![]() ,∴原点
,∴原点![]() 到直线
到直线![]() 的距离的取值范围是
的距离的取值范围是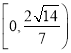
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合A={x|1<x<3},集合B={x|2m<x<1-m}.
(1)当m=-1时,求A∪B;
(2)若AB,求实数m的取值范围;
(3)若A∩B=,求实数m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
直角坐标系中曲线
 的参数方程
的参数方程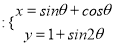 (
(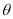 为参数),在以坐标原点为极点,
为参数),在以坐标原点为极点, 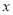 轴正半轴为极轴的极坐标系中,
轴正半轴为极轴的极坐标系中, 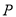 点的极坐标
点的极坐标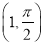 ,在平面直角坐标系中,直线
,在平面直角坐标系中,直线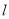 经过点
经过点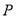 ,倾斜角为
,倾斜角为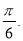
(1)写出曲线
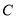 的直角坐标方程和直线
的直角坐标方程和直线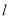 的参数方程;
的参数方程;(2)设直线
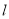 与曲线
与曲线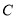 相交于
相交于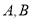 两点,求
两点,求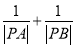 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆内接△ABC中,D为BC上一点,且△ADC为正三角形,点E为BC的延长线上一点,AE为圆O的切线.

(1)求∠BAE 的度数;
(2)求证:
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列结论:
①y=x2+1,x∈[﹣1,2],y的值域[2,5]是;
②幂函数图象一定不过第四象限;
③函数f(x)=loga(2x﹣1)﹣1的图象过定点(1,0);
④若loga >1,则a的取值范围是(
>1,则a的取值范围是(  ,1);
,1);
⑤函数f(x)=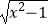 +
+ 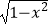 是既奇又偶的函数;
是既奇又偶的函数;
其中正确的序号是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,
中,  ,
, 
 ,
,  平面
平面 ,
,  .设
.设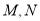 分别为
分别为 的中点.
的中点.
(1)求证:平面
 ∥平面
∥平面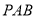 ;
;(2)求二面角
 的平面角的余弦值.
的平面角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
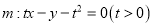 与椭圆
与椭圆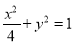 交于
交于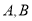 两点,与
两点,与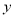 轴交于
轴交于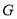 点,
点, 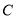 为弦
为弦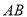 的中点,直线
的中点,直线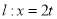 分别与直线
分别与直线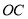 和直线
和直线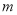 交于
交于 两点.
两点.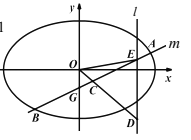
(1)求直线
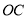 的斜率和直线
的斜率和直线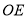 的斜率之积;
的斜率之积;(2)分别记
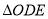 和
和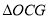 的面积为
的面积为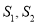 ,是否存在正数
,是否存在正数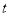 ,使得
,使得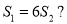 若存在,求出
若存在,求出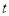 的取值;若不存在,说明理由.
的取值;若不存在,说明理由.
相关试题

