【题目】已知双曲线![]() (
(![]() ,
, ![]() )的左、右焦点分别为
)的左、右焦点分别为![]() 、
、![]() ,过
,过![]() 的直线交双曲线右支于
的直线交双曲线右支于![]() ,
, ![]() 两点,且
两点,且![]() ,若
,若![]() ,则双曲线的离心率为__________.
,则双曲线的离心率为__________.
参考答案:
【答案】![]()
【解析】可设![]() 为双曲线右支上一点,由
为双曲线右支上一点,由![]() ,在直角三角形
,在直角三角形![]() 中,
中, ![]() ,由双曲线的定义可得:
,由双曲线的定义可得: ![]() ,由
,由![]() ,即有
,即有![]() ,即为
,即为![]() ,
, ![]() ,解得
,解得![]() ,
, ![]() ,由勾股定理可得:
,由勾股定理可得: 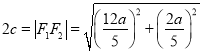
![]() ,可得
,可得![]() ,故答案为
,故答案为![]() .
.
【 方法点睛】本题主要考查双曲线的定义及离心率,属于难题. 离心率的求解在圆锥曲线的考查中是一个重点也是难点,一般求离心率有以下几种情况:①直接求出![]() ,从而求出
,从而求出![]() ; ②构造
; ②构造![]() 的齐次式,求出
的齐次式,求出![]() ;③ 采用离心率的定义以及圆锥曲线的定义来求解;④ 根据圆锥曲线的统一定义求解.本题中,根据双曲线的定义及勾股定理可以找出
;③ 采用离心率的定义以及圆锥曲线的定义来求解;④ 根据圆锥曲线的统一定义求解.本题中,根据双曲线的定义及勾股定理可以找出![]() 之间的关系,求出离心率
之间的关系,求出离心率![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】遂宁市观音湖港口船舶停靠的方案是先到先停.
(1)若甲乙两艘船同时到达港口,双方约定各派一名代表从1,2,3,4,5中各随机选一个数(甲、乙选取的数互不影响),若两数之和为偶数,则甲先停靠;若两数之和为奇数,则乙先停靠,这种规则是否公平?请说明理由.
(2)根据以往经验,甲船将于早上7:00~8:00到达,乙船将于早上7:30~8:30到达,请求出甲船先停靠的概率
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆心在
 轴上的圆
轴上的圆 与直线
与直线 切于点
切于点 .
.(1)求圆
 的标准方程;
的标准方程;(2)已知
 ,经过原点,且斜率为正数的直线
,经过原点,且斜率为正数的直线 与圆
与圆 交于
交于 两点.
两点.(ⅰ)求证:
 为定值;
为定值;(ⅱ)求
 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知三棱锥
 中,
中,  ,
, 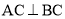 ,
,  为
为 中点,
中点,  为
为 中点,且
中点,且 为正三角形.
为正三角形.(1)求证:
 平面
平面 ;
;(2)若
 ,
,  ,求三棱锥
,求三棱锥 的体积.
的体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知命题
 :
:  表示双曲线,命题
表示双曲线,命题 :
:  表示椭圆。
表示椭圆。(1)若命题
 与命题
与命题 都为真命题,则
都为真命题,则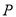 是
是 的什么条件?
的什么条件?(请用简要过程说明是“充分不必要条件”、“必要不充分条件”、“充要条件”和“既不充分也不必要条件”中的哪一个)
(2)若
 为假命题,且
为假命题,且 为真命题,求实数
为真命题,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知平面上的三点
 、
、 、
、 .
.(1)求以
 、
、 为焦点且过点
为焦点且过点 的椭圆的标准方程;
的椭圆的标准方程;(2)设点
 、
、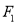 、
、 关于直线
关于直线 的对称点分别为
的对称点分别为 、
、 、
、 ,求以
,求以 、
、 为焦点且过点
为焦点且过点 的双曲线的标准方程.
的双曲线的标准方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 :
:  (
( )的焦点为
)的焦点为 ,点
,点 在抛物线
在抛物线 上,且
上,且 ,直线
,直线 与抛物线
与抛物线 交于
交于 ,
, 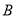 两点,
两点,  为坐标原点.
为坐标原点.(1)求抛物线
 的方程;
的方程;(2)求
 的面积.
的面积.
相关试题

