【题目】如图,已知三棱锥![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 为
为![]() 中点,
中点, ![]() 为
为![]() 中点,且
中点,且![]() 为正三角形.
为正三角形.
(1)求证: ![]() 平面
平面![]() ;
;
(2)若![]() ,
, ![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.

参考答案:
【答案】(1)见解析(2) ![]()
【解析】试题分析:(1)根据![]() 为等边三角形和
为等边三角形和![]() 为中点得到
为中点得到![]() ,而
,而![]() 为
为![]() 的中位线,故而
的中位线,故而![]() ,所以
,所以![]() ,结合
,结合![]() 得到
得到![]() 平面
平面![]() ,故
,故![]() ,而
,而![]() ,所以
,所以![]() 平面
平面![]() .(2)棱锥
.(2)棱锥![]() 的体积可以转化为棱锥
的体积可以转化为棱锥![]() 的体积,由(1)可以得到
的体积,由(1)可以得到![]() 到平面
到平面![]() 的距离为
的距离为![]() 且
且![]() ,而
,而![]() 为等腰三角形且
为等腰三角形且![]() ,从而
,从而![]() 到边
到边![]() 的距离为
的距离为![]() ,故可以
,故可以![]() 的面积,从而利用棱锥的体积公式计算即可.
的面积,从而利用棱锥的体积公式计算即可.
解析:(1)证明:因为![]() 为正三角形,且
为正三角形,且![]() 为
为![]() 中点,所以
中点,所以![]() ,又
,又![]() 为
为![]() 的中点,
的中点, ![]() 为
为![]() 中点,所以
中点,所以![]() .故
.故![]() ,又
,又![]() ,
, ![]() ,故
,故![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() .又因为
.又因为![]() ,
, ![]() ,所以
,所以![]() 平面
平面![]() .
.
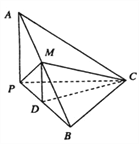
(2)解:由题设有![]() ,
, ![]() ,
, ![]() ,在直角三角形
,在直角三角形![]() 中,
中, ![]() 为斜边
为斜边![]() 的中点,故
的中点,故![]() ,在直角三角形
,在直角三角形![]() 中,
中, ![]() ,又三角形
,又三角形![]() 为等腰三角形,腰长
为等腰三角形,腰长![]() ,底边
,底边![]() ,所以
,所以![]() 边上的高为
边上的高为![]() ,所以
,所以![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知{an}为等差数列,公差为d,且0<d<1,a5≠
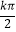 (k∈Z),sin2a3+2sina5cosa5=sin2a7 , 函数f(x)=dsin(wx+4d)(w>0)满足:在
(k∈Z),sin2a3+2sina5cosa5=sin2a7 , 函数f(x)=dsin(wx+4d)(w>0)满足:在 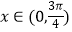 上单调且存在
上单调且存在 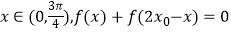 ,则w范围是 .
,则w范围是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】遂宁市观音湖港口船舶停靠的方案是先到先停.
(1)若甲乙两艘船同时到达港口,双方约定各派一名代表从1,2,3,4,5中各随机选一个数(甲、乙选取的数互不影响),若两数之和为偶数,则甲先停靠;若两数之和为奇数,则乙先停靠,这种规则是否公平?请说明理由.
(2)根据以往经验,甲船将于早上7:00~8:00到达,乙船将于早上7:30~8:30到达,请求出甲船先停靠的概率
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆心在
 轴上的圆
轴上的圆 与直线
与直线 切于点
切于点 .
.(1)求圆
 的标准方程;
的标准方程;(2)已知
 ,经过原点,且斜率为正数的直线
,经过原点,且斜率为正数的直线 与圆
与圆 交于
交于 两点.
两点.(ⅰ)求证:
 为定值;
为定值;(ⅱ)求
 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知双曲线
 (
(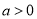 ,
,  )的左、右焦点分别为
)的左、右焦点分别为 、
、 ,过
,过 的直线交双曲线右支于
的直线交双曲线右支于 ,
,  两点,且
两点,且 ,若
,若 ,则双曲线的离心率为__________.
,则双曲线的离心率为__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知命题
 :
:  表示双曲线,命题
表示双曲线,命题 :
:  表示椭圆。
表示椭圆。(1)若命题
 与命题
与命题 都为真命题,则
都为真命题,则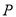 是
是 的什么条件?
的什么条件?(请用简要过程说明是“充分不必要条件”、“必要不充分条件”、“充要条件”和“既不充分也不必要条件”中的哪一个)
(2)若
 为假命题,且
为假命题,且 为真命题,求实数
为真命题,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知平面上的三点
 、
、 、
、 .
.(1)求以
 、
、 为焦点且过点
为焦点且过点 的椭圆的标准方程;
的椭圆的标准方程;(2)设点
 、
、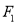 、
、 关于直线
关于直线 的对称点分别为
的对称点分别为 、
、 、
、 ,求以
,求以 、
、 为焦点且过点
为焦点且过点 的双曲线的标准方程.
的双曲线的标准方程.
相关试题

