【题目】已知函数f(x)=a﹣![]() (a∈R)
(a∈R)
(Ⅰ)判断函数f(x)在R上的单调性,并用单调函数的定义证明;
(Ⅱ)是否存在实数a使函数f(x)为奇函数?若存在,求出a的值;若不存在,请说明理由.
参考答案:
【答案】(1)见解析(2)a=1.
【解析】试题分析:(1)定义域任取两个变量x1,x2,并设x1<x2,作差f(x1)﹣f(x2),差式变形成分式,利用指数函数的单调性判断正负,进而得函数的单调性。(2)因为定义域为R,所以![]() ,解方程求得
,解方程求得![]() 。利用奇函数定义证明。
。利用奇函数定义证明。
试题解析:(1)证明:函数f(x)的定义域为R,对任意x1,x2∈R,设x1<x2,
则f(x1)﹣f(x2)= =
= .
.
∵y=2x是R上的增函数,且x1<x2,
∴2x1﹣2x2<0,
∴f(x1)﹣f(x2)<0.
即f(x1)<f(x2),
∴函数f(x)为R上的增函数;
(2)解:若函数f(x)为奇函数,
则f(0)=a﹣1=0,
∴a=1.
当a=1时,f(x)=1﹣![]() .
.
∴f(﹣x)=![]() =﹣f(x),
=﹣f(x),
此时f(x)为奇函数,满足题意,
∴a=1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x2-1,g(x)=

(1)求f[g(2)]和g[f(2)]的值;
(2)求f[g(x)]和g[f(x)]的表达式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
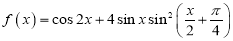 .
.(1)将函数
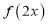 的图像向右平移
的图像向右平移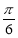 个单位得到函数
个单位得到函数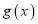 的图像,若
的图像,若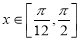 ,求函数
,求函数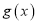 的值域;
的值域;(2)已知
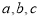 ,分别为
,分别为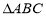 中角
中角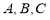 的对边,且满足
的对边,且满足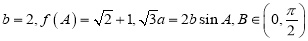 ,求
,求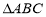 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】随着网络的发展,人们可以在网络上购物、玩游戏、聊天、导航等,所以人们对上网流量的需求越来越大.某电信运营商推出一款新的“流量包”套餐.为了调查不同年龄的人是否愿意选择此款“流量包”套餐,随机抽取50个用户,按年龄分组进行访谈,统计结果如右表.
组
号
年龄
访谈
人数
愿意
使用
1
[18,28)
4
4
2
[28,38)
9
9
3
[38,48)
16
15
4
[48,58)
15
12
5
[58,68)
6
2
(Ⅰ)若在第2、3、4组愿意选择此款“流量包”套餐的人中,用分层抽样的方法抽取12人,则各组应分别抽取多少人?
(Ⅱ)若从第5组的被调查者访谈人中随机选取2人进行追踪调查,求2人中至少有1人愿意选择此款“流量包”套餐的概率.
(Ⅲ)按以上统计数据填写下面2×2列联表,并判断以48岁为分界点,能否在犯错误不超过1%的前提下认为,是否愿意选择此款“流量包”套餐与人的年龄有关?
年龄不低于48岁的人数
年龄低于48岁的人数
合计
愿意使用的人数
不愿意使用的人数
合计
参考公式:
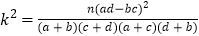 ,其中:n=a+b+c+d.
,其中:n=a+b+c+d.P(k2≥k0)
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k
2.072
2.706
3.841
5.024
6.635
7.879
10.828
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知公比小于1的等比数列
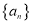 的前
的前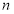 项和为
项和为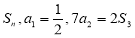 .
.(1)求数列
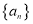 的通项公式;
的通项公式;(2)设
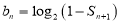 ,若
,若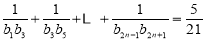 ,求
,求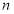 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}中,a1=3,a10=21,通项an相应的函数是一次函数.
(1) 求数列{an}的通项公式;
(2) 若{bn}是由a2,a4,a6,a8,…组成,试求数列{bn}的通项公式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知(x,y)在映射f的作用下的像是(x+y,xy).
(1)求(-2,3)在f作用下的像;
(2)若在f作用下的像是(2,-3),求它的原像.
相关试题

