【题目】已知函数f(x)=ex-e-x(x∈R,且e为自然对数的底数).
(1)判断函数f(x)的奇偶性与单调性.
(2)是否存在实数t,使不等式f(x-t)+f(x2-t2)≥0对一切x都成立?若存在,求出t;若不存在,请说明理由.
参考答案:
【答案】见解析
【解析】(1)∵f(x)=ex-![]()
![]() ,且y=ex是增函数,
,且y=ex是增函数,
y=-![]()
![]() 是增函数,∴f(x)是增函数.
是增函数,∴f(x)是增函数.
∵f(x)的定义域为R,
且f(-x)=e-x-ex=-f(x),
∴f(x)是奇函数.
(2)由(1)知f(x)是增函数和奇函数,
由f(x-t)+f(x2-t2)≥0对x∈R恒成立,
则f(x-t)≥f(t2-x2).
∴t2-x2≤x-tx2+x≥t2+t对x∈R恒成立![]()
![]() ≤
≤![]()
![]() min对一切x∈R恒成立
min对一切x∈R恒成立![]()
![]() ≤0t=-
≤0t=-![]() .
.
即存在实数t=-![]() ,使不等式f(x-t)+f(x2-t2)≥0对一切x都成立.
,使不等式f(x-t)+f(x2-t2)≥0对一切x都成立.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,棱锥P—ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD=
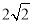 .求二面角P—BC—D余弦值的大小.
.求二面角P—BC—D余弦值的大小. 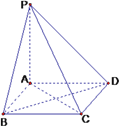
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=
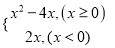 ,
,(1)画出函数y=f(x)的图象;
(2)讨论方程|f(x)|=a的解的个数.(只写明结果,无需过程)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列给出的输入语句、输出语句和赋值语句:
(1)输出语句INPUT
 ,b,c
,b,c(2)输入语句INPUT
 =3
=3(3)赋值语句3=A
(4)赋值语句A=B=C
则其中正确的个数是( )
(A)0 (B)1 (C)2 (D)3
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
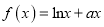 ,
, 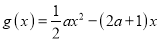 .
.(1)若
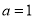 ,证明:
,证明: 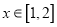 时,
时, 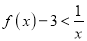 成立;
成立;(2)讨论函数
 的单调性;
的单调性; -
科目: 来源: 题型:
查看答案和解析>>【题目】随着手机的发展,“微信”越来越成为人们交流的一种方式.某机构对“使用微信交流”的态度进行调查,随机抽取了50人,他们年龄的频数分布及对“使用微信交流”赞成人数如下表.
年龄(单位:岁)
[15,25)
[25,35)
[35,45)
[45,55)
[55,65)
[65,75)
频数
5
10
15
10
5
5
赞成人数
5
10
12
7
2
1
(Ⅰ)若以“年龄45岁为分界点”,由以上统计数据完成下面
 列联表,并判断是否有99%的把握认为“使用微信交流”的态度与人的年龄有关;
列联表,并判断是否有99%的把握认为“使用微信交流”的态度与人的年龄有关;年龄不低于45岁的人数
年龄低于45岁的人数
合计
赞成
不赞成
合计
(Ⅱ)若从年龄在[25,35)和[55,65)的被调查人中按照分层抽样的方法选取6人进行追踪调查,并给予其中3人“红包”奖励,求3人中至少有1人年龄在[55,65)的概率.
参考数据如下:
附临界值表:
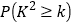
0.15
0.10
0.05
0.025
0.010
0.005
0.001
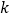
2.072
2.706
3.841
5.024
6.635
7.879
10.828
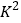 的观测值:
的观测值: 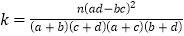 (其中
(其中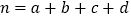 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】定义在[-1,1]上的奇函数f(x),已知当x∈[-1,0]时,f(x)=
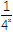 -
-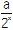 (a∈R).
(a∈R).(1)写出f(x)在[0,1]上的解析式;
(2)求f(x)在[0,1]上的最大值.
相关试题

