【题目】已知函数![]() ,
,
![]()
(Ⅰ)若![]() 讨论
讨论![]() 的单调性;
的单调性;
(Ⅱ)若过点![]() 可作函数
可作函数![]() 图象的两条不同切线,求实数
图象的两条不同切线,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(Ⅰ) 见解析;(Ⅱ) ![]() .
.
【解析】试题分析:(Ⅰ)分![]() 讨论函数
讨论函数![]() 的单调性;(Ⅱ)求出经过点P的切线方程,由
的单调性;(Ⅱ)求出经过点P的切线方程,由![]() 在切线上,得到
在切线上,得到![]() ,问题转化为
,问题转化为![]() 有两个不同的正数解,令
有两个不同的正数解,令![]() ,由单调性求出a的范围.
,由单调性求出a的范围.
试题解析:(Ⅰ) ![]()
![]()
①当![]() 时,
时, 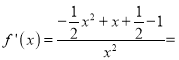
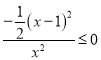 ,此时,
,此时, ![]()
![]() 上是减函数
上是减函数
②当![]() 时,
时, ![]()
![]() ,得
,得![]() ;
;
![]()
![]() ,得
,得![]()
此时, ![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 是增函数
是增函数
③当![]() 时,解
时,解![]() ,得,
,得,
此时, ![]() 在
在![]() 和
和![]() 是减函数,在
是减函数,在![]() 是增函数
是增函数
(Ⅱ)设点![]() 是函数
是函数![]() 图象上的切点,则过点
图象上的切点,则过点![]() 的切线的斜率为
的切线的斜率为![]() ,
,
所以过点![]() 的切线方程为
的切线方程为![]() .
.
因为点![]() 在切线上,所以
在切线上,所以![]()
即![]() .
.
若过点![]() 可作函数
可作函数![]() 图象的两条不同切线,
图象的两条不同切线,
则方程![]() 有两个不同的正数解.
有两个不同的正数解.
令![]() ,则函数
,则函数![]() 与
与![]() 轴正半轴有两个不同的交点.
轴正半轴有两个不同的交点.
令![]() ,解得
,解得![]() 或
或![]() .
.
因为![]() ,
, ![]() ,
,
所以必须![]() ,即
,即![]() .
.
所以实数![]() 的取值范围为
的取值范围为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某蛋糕店每天做若干个生日蛋糕,每个制作成本为50元,当天以每个100元售出,若当天白天售不出,则当晚以30元/个价格作普通蛋糕低价售出,可以全部售完.
(1)若蛋糕店每天做20个生日蛋糕,求当天的利润
 (单位:元)关于当天生日蛋糕的需求量
(单位:元)关于当天生日蛋糕的需求量 (单位:个,
(单位:个,  )的函数关系;
)的函数关系;(2)蛋糕店记录了100天生日蛋糕的日需求量(单位:个)整理得下表:

(ⅰ)假设蛋糕店在这100天内每天制作20个生日蛋糕,求这100天的日利润(单位:元)的平均数;
(ⅱ)若蛋糕店一天制作20个生日蛋糕,以100天记录的各需求量的频率作为概率,求当天利润不少于900元的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
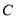 过两点
过两点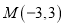 ,
, 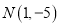 ,且圆心
,且圆心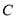 在直线
在直线 上.
上.(Ⅰ)求圆
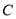 的标准方程;
的标准方程;(Ⅱ)直线
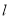 过点
过点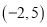 且与圆
且与圆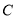 有两个不同的交点
有两个不同的交点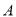 ,
, 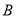 ,若直线
,若直线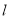 的斜率
的斜率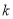 大于0,求
大于0,求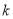 的取值范围;
的取值范围;(Ⅲ)在(Ⅱ)的条件下,是否存在直线
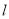 使得弦
使得弦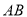 的垂直平分线过点
的垂直平分线过点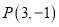 ,若存在,求出直线
,若存在,求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】从参加某次高中英语竞赛的学生中抽出100名,将其成绩整理后,绘制频率分布直方图(如图所示).其中样本数据分组区间为:
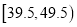 ,
, 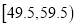 ,
, 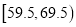 ,
, 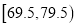 ,
, 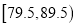 ,
, 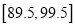 .
.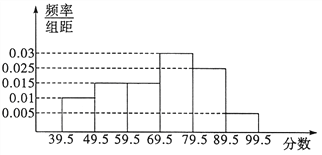
(Ⅰ)试求图中
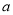 的值,并计算区间
的值,并计算区间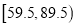 上的样本数据的频率和频数;
上的样本数据的频率和频数;(Ⅱ)试估计这次英语竞赛成绩的众数、中位数及平均成绩(结果精确到
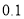 ).
).注:同一组数据用该组区间的中点值作为代表
-
科目: 来源: 题型:
查看答案和解析>>【题目】在三角形ABC中,分别根据下列条件解三角形,其中有两个解的是( )
A.a=8b=16A=30°
B.a=25b=30A=150°
C.a=30b=40A=30°
D.a=72b=60A=135° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三棱柱
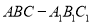 中,底面
中,底面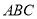 为正三角形,
为正三角形, 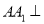 底面
底面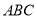 ,且
,且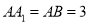 ,
, 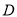 是
是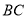 的中点.
的中点.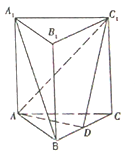
(1)求证:
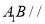 平面
平面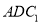 ;
; (2)求证:平面
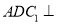 平面
平面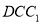 ;
;(3)在侧棱
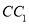 上是否存在一点
上是否存在一点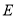 ,使得三棱锥
,使得三棱锥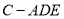 的体积是
的体积是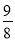 ?若存在,求出
?若存在,求出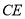 的长;若不存在,说明理由.
的长;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】等差数列{an}的前n项和Sn , 若a3+a7﹣a10=8,a11﹣a4=4,则S13等于( )
A.152
B.154
C.156
D.158
相关试题

