【题目】在三角形ABC中,分别根据下列条件解三角形,其中有两个解的是( )
A.a=8b=16A=30°
B.a=25b=30A=150°
C.a=30b=40A=30°
D.a=72b=60A=135°
参考答案:
【答案】C
【解析】解:由正弦定理可得 ![]() ,若A成立,a=8,b=16,A=30°,有
,若A成立,a=8,b=16,A=30°,有 ![]() =
= ![]() ,∴sinB=1,∴B=90°,故三角形ABC有唯一解. 若B成立,a=25,b=30,A=150°,有
,∴sinB=1,∴B=90°,故三角形ABC有唯一解. 若B成立,a=25,b=30,A=150°,有 ![]() =
= ![]() ,∴sinB=
,∴sinB= ![]() ,又b>a,故 B>150°,故三角形ABC无解.
,又b>a,故 B>150°,故三角形ABC无解.
若C成立,a=30,b=40,A=30°,有 ![]() =
= ![]() ,∴sinB=
,∴sinB= ![]() ,又b>a,故 B>A,故B可以是锐角,也可以是钝角,故三角形ABC有两个解.
,又b>a,故 B>A,故B可以是锐角,也可以是钝角,故三角形ABC有两个解.
若D 成立,a=72,b=60,A=135°,有 ![]() =
= ![]() ,∴sinB=
,∴sinB= ![]() ,由于B<A,故B为锐角,故三角形ABC有唯一解.
,由于B<A,故B为锐角,故三角形ABC有唯一解.
故选C.
由正弦定理可得 ![]() ,根据条件求得sinB的值,根据b与a 的大小判断角B的大小,从而判断三角形ABC 的解的个数.
,根据条件求得sinB的值,根据b与a 的大小判断角B的大小,从而判断三角形ABC 的解的个数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
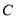 过两点
过两点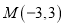 ,
, 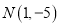 ,且圆心
,且圆心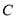 在直线
在直线 上.
上.(Ⅰ)求圆
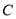 的标准方程;
的标准方程;(Ⅱ)直线
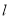 过点
过点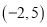 且与圆
且与圆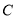 有两个不同的交点
有两个不同的交点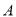 ,
, 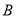 ,若直线
,若直线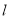 的斜率
的斜率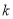 大于0,求
大于0,求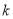 的取值范围;
的取值范围;(Ⅲ)在(Ⅱ)的条件下,是否存在直线
 使得弦
使得弦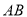 的垂直平分线过点
的垂直平分线过点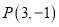 ,若存在,求出直线
,若存在,求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】从参加某次高中英语竞赛的学生中抽出100名,将其成绩整理后,绘制频率分布直方图(如图所示).其中样本数据分组区间为:
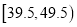 ,
, 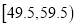 ,
, 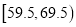 ,
, 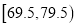 ,
, 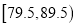 ,
, 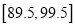 .
.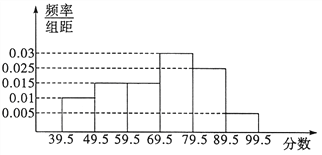
(Ⅰ)试求图中
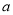 的值,并计算区间
的值,并计算区间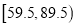 上的样本数据的频率和频数;
上的样本数据的频率和频数;(Ⅱ)试估计这次英语竞赛成绩的众数、中位数及平均成绩(结果精确到
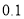 ).
).注:同一组数据用该组区间的中点值作为代表
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
,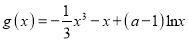
(Ⅰ)若
 讨论
讨论 的单调性;
的单调性;(Ⅱ)若过点
 可作函数
可作函数 图象的两条不同切线,求实数
图象的两条不同切线,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三棱柱
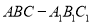 中,底面
中,底面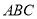 为正三角形,
为正三角形, 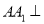 底面
底面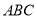 ,且
,且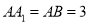 ,
, 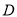 是
是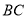 的中点.
的中点.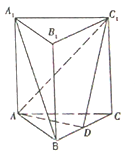
(1)求证:
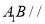 平面
平面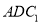 ;
; (2)求证:平面
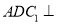 平面
平面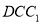 ;
;(3)在侧棱
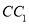 上是否存在一点
上是否存在一点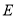 ,使得三棱锥
,使得三棱锥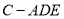 的体积是
的体积是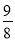 ?若存在,求出
?若存在,求出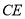 的长;若不存在,说明理由.
的长;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】等差数列{an}的前n项和Sn , 若a3+a7﹣a10=8,a11﹣a4=4,则S13等于( )
A.152
B.154
C.156
D.158 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x﹣[x],其中[x]表示不超过实数x的最大整数.若关于x的方程f(x)=kx+k有三个不同的实根,则实数k的取值范围是( )
A.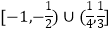
B.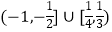
C.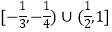
D.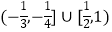
相关试题

