【题目】已知圆C1:x2+y2﹣3x﹣3y+3=0,圆C2:x2+y2﹣2x﹣2y=0.
(1)求两圆的公共弦所在的直线方程及公共弦长.
(2)求过两圆交点且面积最小的圆的方程.
参考答案:
【答案】
(1)解:设两圆的交点为A(x1,y1),B(x2,y2),
则A、B两点的坐标是圆C1:x2+y2﹣3x﹣3y+3=0,圆C2:x2+y2﹣2x﹣2y=0,联立方程组的解,
两方程相减得:x+y﹣3=0,
∵A、B两点的坐标都满足该方程,∴x+y﹣3=0为所求.
将圆C2的方程化为标准形式,(x﹣1)2+(y﹣1)2=2,∴圆心C2(1,1),半径r= ![]() .
.
圆心C2到直线AB的距离d= ![]() =
= ![]() ,|AB|=
,|AB|= ![]() .
.
即两圆的公共弦长为 ![]()
(2)解:C1( ![]() ,
, ![]() ),C2(1,1),直线C1C2方程:x﹣y=0.
),C2(1,1),直线C1C2方程:x﹣y=0.
![]() ,交点为
,交点为 ![]() ,
,
即为圆的圆心,半径r= ![]() ,
,
所以圆的方程是: ![]()
【解析】(1)两方程相减求两圆的公共弦所在的直线方程,利用勾股定理公共弦长.(2)直线C1C2方程:x﹣y=0. ![]() ,交点为
,交点为 ![]() ,即为圆的圆心,半径r=
,即为圆的圆心,半径r= ![]() ,即可求过两圆交点且面积最小的圆的方程.
,即可求过两圆交点且面积最小的圆的方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合A={x|0<ax+1≤5},B={x|﹣
 <x≤2}.
<x≤2}.
(1)当a=1时,判断集合BA是否成立?
(2)若AB,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 是定义在(﹣1,1)上的奇函数,且f(1)=1.
是定义在(﹣1,1)上的奇函数,且f(1)=1.
(1)求函数f(x)的解析式;
(2)判断并证明f(x)在(﹣1,1)上的单调性. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系
 中,直线
中,直线 的参数方程为
的参数方程为 (
( 为参数).以原点
为参数).以原点 为极点,
为极点,  轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线 的极坐标方程为
的极坐标方程为 .直线
.直线 交曲线
交曲线 于
于 两点.
两点.(1)写出直线
 的极坐标方程和曲线
的极坐标方程和曲线 的直角坐标方程;
的直角坐标方程;(2)设点
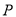 的直角坐标为
的直角坐标为 ,求点
,求点 到
到 两点的距离之积.
两点的距离之积. -
科目: 来源: 题型:
查看答案和解析>>【题目】某消费品专卖店的经营资料显示如下:
①这种消费品的进价为每件14元;
②该店月销售量Q(百件)与销售价格P(元)满足的函数关系式为Q=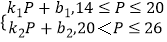 ,点(14,22),(20,10),(26,1)在函数的图象上;
,点(14,22),(20,10),(26,1)在函数的图象上;
③每月需各种开支4400元.
(1)求月销量Q(百件)与销售价格P(元)的函数关系;
(2)当商品的价格为每件多少元时,月利润最大?并求出最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校
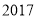 届高三文(1)班在一次数学测验中,全班
届高三文(1)班在一次数学测验中,全班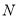 名学生的数学成绩的频率分布直方图如下,已知分数在
名学生的数学成绩的频率分布直方图如下,已知分数在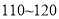 的学生数有
的学生数有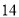 人.
人.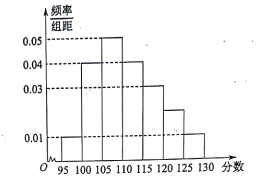
(1)求总人数
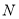 和分数在
和分数在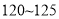 的人数
的人数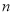 ;
;(2)利用频率分布直方图,估算该班学生数学成绩的众数和中位数各是多少?
(3)现在从比分数在
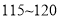 名学生(男女生比例为
名学生(男女生比例为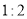 )中任选
)中任选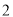 人,求其中至多含有
人,求其中至多含有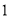 名男生的概率.
名男生的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=log2(4x+1)﹣x,g(x)=log2a+log2(2x﹣
 )(a>0,x>1).
)(a>0,x>1).
(1)证明函数f(x)为偶函数;
(2)若函数f(x)﹣g(x)只有一个零点,求实数a的取值范围.
相关试题

