【题目】已知函数f(x)= ![]() 是定义在(﹣1,1)上的奇函数,且f(1)=1.
是定义在(﹣1,1)上的奇函数,且f(1)=1.
(1)求函数f(x)的解析式;
(2)判断并证明f(x)在(﹣1,1)上的单调性.
参考答案:
【答案】
(1)解:∵函数f(x)= ![]() 是定义在(﹣1,1)上的奇函数,
是定义在(﹣1,1)上的奇函数,
∴f(0)=0,
又∵f(1)=1.
∴ 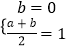 ,
,
解得: ![]() ,
,
∴函数f(x)= ![]()
(2)解:f(x)在(﹣1,1)上单调递增,理由如下:
∵f′(x)= ![]() ,
,
当x∈(﹣1,1)时,f′(x)≥0恒成立,
故f(x)在(﹣1,1)上单调递增
【解析】(1)根据奇函数的特性,可得f(0)=0,结合f(1)=1,构造方程组,解得函数f(x)的解析式;(2)利用导数法,可证得f(x)在(﹣1,1)上单调递增.
【考点精析】本题主要考查了函数单调性的判断方法和利用导数研究函数的单调性的相关知识点,需要掌握单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较;一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减才能正确解答此题.
在这个区间单调递减才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】圆心在直线x﹣2y=0上的圆C与y轴的正半轴相切,圆C截x轴所得弦的长为2
 ,求圆C的标准方程.
,求圆C的标准方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=﹣3x2+a(6﹣a)x+c.
(1)当c=19时,解关于a的不等式f(1)>0;
(2)若关于x的不等式f(x)>0的解集是(﹣1,3),求实数a,c的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合A={x|0<ax+1≤5},B={x|﹣
 <x≤2}.
<x≤2}.
(1)当a=1时,判断集合BA是否成立?
(2)若AB,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系
 中,直线
中,直线 的参数方程为
的参数方程为 (
( 为参数).以原点
为参数).以原点 为极点,
为极点,  轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线 的极坐标方程为
的极坐标方程为 .直线
.直线 交曲线
交曲线 于
于 两点.
两点.(1)写出直线
 的极坐标方程和曲线
的极坐标方程和曲线 的直角坐标方程;
的直角坐标方程;(2)设点
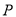 的直角坐标为
的直角坐标为 ,求点
,求点 到
到 两点的距离之积.
两点的距离之积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆C1:x2+y2﹣3x﹣3y+3=0,圆C2:x2+y2﹣2x﹣2y=0.
(1)求两圆的公共弦所在的直线方程及公共弦长.
(2)求过两圆交点且面积最小的圆的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】某消费品专卖店的经营资料显示如下:
①这种消费品的进价为每件14元;
②该店月销售量Q(百件)与销售价格P(元)满足的函数关系式为Q=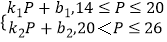 ,点(14,22),(20,10),(26,1)在函数的图象上;
,点(14,22),(20,10),(26,1)在函数的图象上;
③每月需各种开支4400元.
(1)求月销量Q(百件)与销售价格P(元)的函数关系;
(2)当商品的价格为每件多少元时,月利润最大?并求出最大值.
相关试题

