【题目】已知f(x)= ![]() .
.
(1)证明:f(x)是定义域内的增函数;
(2)求f(x)的值域.
参考答案:
【答案】
(1)证明:∵f(x)= ![]() =
= ![]() =1﹣
=1﹣ ![]() .
.
∴f′(x)= ![]() ,
,
∵f′(x)>0恒成立,
故f(x)是定义域R内的增函数
(2)当x→﹣∞时,102x→0, ![]() →2,f(x)→﹣1,
→2,f(x)→﹣1,
当x→+∞时,102x→+∞, ![]() →0,f(x)→1,
→0,f(x)→1,
故f(x)的值域为(﹣1,1)
【解析】(1)求导,根据f′(x)>0恒成立,可得:f(x)是定义域R内的增函数;(2)求出函数在x→﹣∞时和x→+∞时的极限值,进而可得函数的值域.
【考点精析】利用函数的值域和利用导数研究函数的单调性对题目进行判断即可得到答案,需要熟知求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的;一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 的定义域为集合A,B={x∈Z|2<x<10},C={x∈R|x<a或x>a+1}
的定义域为集合A,B={x∈Z|2<x<10},C={x∈R|x<a或x>a+1}
(1)求A,(RA)∩B;
(2)若A∪C=R,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,直线
,直线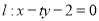 .
.(1)若直线
 与曲线
与曲线 相切,求切点横坐标的值;
相切,求切点横坐标的值;(2)若函数
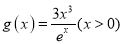 ,求证:
,求证: 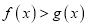 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C的方程为:
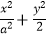 =1(a>0),其焦点在x轴上,离心率e=
=1(a>0),其焦点在x轴上,离心率e= 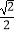 .
.
(1)求该椭圆的标准方程;
(2)设动点P(x0 , y0)满足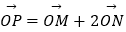 ,其中O为坐标原点,M,N是椭圆C上的点,直线OM与ON的斜率之积为﹣
,其中O为坐标原点,M,N是椭圆C上的点,直线OM与ON的斜率之积为﹣  ,求证:x02+2y02为定值.
,求证:x02+2y02为定值.
(3)在(2)的条件下,问:是否存在两个定点A,B,使得|PA|+|PB|为定值?若存在,给出证明;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知球内接正四棱锥
 的高为
的高为 相交于
相交于 ,球的表面积为
,球的表面积为 ,若
,若 为
为 中点.
中点.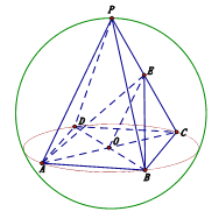
(1)求异面直线
 和
和 所成角的余弦值;
所成角的余弦值;(2)求点
 到平面
到平面 的距离.
的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知双曲线的顶点与焦点分别是椭圆
 =1(a>b>0)的焦点与顶点,若双曲线的两条渐近线与椭圆的交点构成的四边形恰为正方形,则椭圆的离心率为( )
=1(a>b>0)的焦点与顶点,若双曲线的两条渐近线与椭圆的交点构成的四边形恰为正方形,则椭圆的离心率为( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若抛物线C:y=ax2﹣1(a≠0)上有不同两点关于直线l:y+x=0对称,则实数a的取值范围是
相关试题

