【题目】已知球内接正四棱锥![]() 的高为
的高为![]() 相交于
相交于![]() ,球的表面积为
,球的表面积为![]() ,若
,若![]() 为
为![]() 中点.
中点.
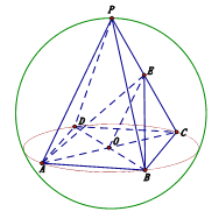
(1)求异面直线![]() 和
和![]() 所成角的余弦值;
所成角的余弦值;
(2)求点![]() 到平面
到平面![]() 的距离.
的距离.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1) 由球的表面积求出球的半径R,设球心为![]() ,则
,则![]() 必在
必在![]() 上,连
上,连![]() ,根据球的性质有
,根据球的性质有![]() ,求解易得底面边长以及侧棱长,则结论易得;(2)证明
,求解易得底面边长以及侧棱长,则结论易得;(2)证明![]() 平面
平面![]() ,则
,则![]() 到平面
到平面![]() 的距离等于
的距离等于![]() 到平面
到平面![]() 的距离,由
的距离,由![]() ,则结论易得.
,则结论易得.
试题解析:由球的表面积公式![]() ,得球的半径
,得球的半径![]() ,
,
设球心为![]() ,在正四棱锥
,在正四棱锥![]() 中,高为
中,高为![]() ,则
,则![]() 必在
必在![]() 上,
上,
连![]() ,则
,则![]() ,
,
则在![]() ,有
,有![]() ,即
,即![]() ,可得正方形
,可得正方形![]() 的边长为
的边长为![]() ,
,
侧棱![]() .
.
(1)在正方形![]() 中,
中, ![]() ,所
,所![]() 以是异面直线
以是异面直线![]() 和
和![]() 所成的角或其补角,
所成的角或其补角,
取![]() 中点
中点![]() ,在等腰
,在等腰![]() 中,可得
中,可得![]() ,斜高
,斜高![]() ,
,
则在![]() 中,
中, ![]() ,
,
所以异面直线![]() 和
和![]() 所成的角的余弦值为
所成的角的余弦值为![]() ;
;
(2)由![]() 为
为![]() 中点,得
中点,得![]() ,
,
且满足![]() 平面
平面![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
所以![]() 到平面
到平面![]() 的距离等于
的距离等于![]() 到平面
到平面![]() 的距离,
的距离,
又因为![]() ,
,
再设![]() 到平面
到平面![]() 的距离为
的距离为![]() ,则由
,则由![]() ,
,
可得![]() ,则
,则![]() ,
,
所以点![]() 到平面
到平面![]() 的距离
的距离![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,直线
,直线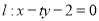 .
.(1)若直线
 与曲线
与曲线 相切,求切点横坐标的值;
相切,求切点横坐标的值;(2)若函数
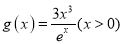 ,求证:
,求证: 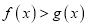 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C的方程为:
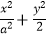 =1(a>0),其焦点在x轴上,离心率e=
=1(a>0),其焦点在x轴上,离心率e= 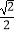 .
.
(1)求该椭圆的标准方程;
(2)设动点P(x0 , y0)满足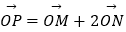 ,其中O为坐标原点,M,N是椭圆C上的点,直线OM与ON的斜率之积为﹣
,其中O为坐标原点,M,N是椭圆C上的点,直线OM与ON的斜率之积为﹣  ,求证:x02+2y02为定值.
,求证:x02+2y02为定值.
(3)在(2)的条件下,问:是否存在两个定点A,B,使得|PA|+|PB|为定值?若存在,给出证明;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=
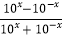 .
.
(1)证明:f(x)是定义域内的增函数;
(2)求f(x)的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知双曲线的顶点与焦点分别是椭圆
 =1(a>b>0)的焦点与顶点,若双曲线的两条渐近线与椭圆的交点构成的四边形恰为正方形,则椭圆的离心率为( )
=1(a>b>0)的焦点与顶点,若双曲线的两条渐近线与椭圆的交点构成的四边形恰为正方形,则椭圆的离心率为( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若抛物线C:y=ax2﹣1(a≠0)上有不同两点关于直线l:y+x=0对称,则实数a的取值范围是
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)是定义在R上的偶函数,且x≤0时,f(x)=log
 (﹣x+1).
(﹣x+1).
(1)求f(x)的解析式;
(2)若f(a﹣1)<﹣1,求实数a的取值范围.
相关试题

