【题目】已知函数![]() ,令
,令![]() ,其中
,其中![]() 是函数
是函数![]() 的导函数.
的导函数.
(1)当![]() 时,求
时,求![]() 的极值;
的极值;
(2)当![]() 时,若存在
时,若存在![]() ,使得
,使得![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)极小值![]() ,无极大值.(2)
,无极大值.(2)![]()
【解析】
试题分析:(1)先求函数导数:![]() ,再求导函数零点
,再求导函数零点![]() 。列表分析可得函数单调性变化规律,进而确定极值(2)先将不等式存在性问题转化为对应函数最值问题:
。列表分析可得函数单调性变化规律,进而确定极值(2)先将不等式存在性问题转化为对应函数最值问题:![]() ,即
,即![]() ,
,![]() ,再利用变量分离法将不等式恒成立问题转化为对应函数最值问题
,再利用变量分离法将不等式恒成立问题转化为对应函数最值问题![]() 最大值,最后根据导数求函数最值
最大值,最后根据导数求函数最值
试题解析:(1)依题意![]() ,则
,则![]() ,当
,当![]() 时,
时,![]() ,令
,令![]() ,解得
,解得![]() .当
.当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .所以
.所以![]() 的单调递减区间为
的单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() .所以
.所以![]() 时,
时,
![]() 取得极小值
取得极小值![]() ,无极大值.
,无极大值.
(2)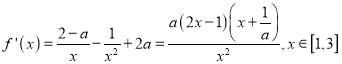 ,当
,当![]() 时,即:
时,即:![]() 时,恒有
时,恒有![]() 成立.所以在
成立.所以在![]() 上是单调递减.所以
上是单调递减.所以![]() ,所以
,所以![]() ,因为存在
,因为存在![]() ,使得
,使得![]() 恒成立,所以
恒成立,所以![]() ,整理得
,整理得![]() ,
,
又![]() .令
.令![]() ,则
,则![]() ,构造函数
,构造函数![]() ,当
,当![]() 时,
时,![]() ; 当
; 当![]() 时,
时,![]() ,
,
此时函数单调递增,当![]() 时,
时,![]() ,此时函数单调递减,所以
,此时函数单调递减,所以![]() ,
,
所以![]() 的取值范围为
的取值范围为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的左右顶点为
的左右顶点为 、
、 ,左右焦点为
,左右焦点为 ,其长半轴的长等于焦距,点
,其长半轴的长等于焦距,点 是椭圆上的动点,
是椭圆上的动点, 面积的最大值为
面积的最大值为 .
.(1)求椭圆的方程;
(2)设
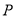 为直线
为直线 上不同于点
上不同于点 的任意一点,若直线
的任意一点,若直线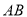 、
、 分别与椭圆交于异于
分别与椭圆交于异于 、
、 的点
的点 、
、 ,判断点
,判断点 与以
与以 为直径的圆的位置关系.
为直径的圆的位置关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】设命题p:x>0,x-lnx>0,则¬p为
A. x0>0,x0-lnx0>0 B. x0>0,x0-lnx0≤0
C. x>0,x-lnx<0 D. x>0,x-lnx≤0
-
科目: 来源: 题型:
查看答案和解析>>【题目】圆x2+y2-4x+6y=0和圆x2+y2-6x=0交于A,B两点,则直线AB的方程是( )
A. x+y+3=0 B. 3x-y-9=0
C. x+3y=0 D. 4x-3y+7=0
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为
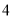 的菱形
的菱形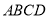 中,
中,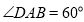 ,点
,点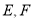 分别是边
分别是边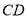 ,
,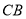 的中点,
的中点,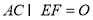 ,沿
,沿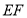 将
将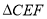 翻折到
翻折到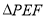 ,连接
,连接 ,得到如图的五棱锥
,得到如图的五棱锥 ,且
,且 .
.
(1)求证:
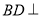 平面
平面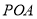 ;
;(2)求二面角
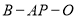 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义在
 上的函数
上的函数 是奇函数.
是奇函数.(1)求实数
 ,
, 的值;
的值;(2)判断
 的单调性,并用函数的单调性定义证明你的结论.
的单调性,并用函数的单调性定义证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
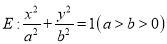 的左、右焦点分别是
的左、右焦点分别是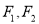 ,离心率
,离心率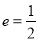 ,过点
,过点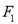 且垂直于
且垂直于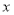 轴的直线被椭圆
轴的直线被椭圆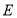 截得的线段长为
截得的线段长为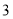 .
.(1)求椭圆
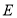 的方程;
的方程;(2)若直线
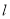 过椭圆
过椭圆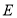 的右焦点
的右焦点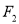 ,且与
,且与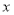 轴不重合,交椭圆
轴不重合,交椭圆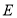 于
于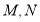 两点,过点
两点,过点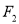 且与
且与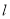 垂直的直线与圆
垂直的直线与圆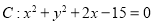 交于
交于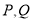 两点,求四边形
两点,求四边形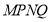 面积的取值范围.
面积的取值范围.
相关试题

