【题目】已知椭圆![]() 的左、右焦点分别是
的左、右焦点分别是![]() ,离心率
,离心率![]() ,过点
,过点![]() 且垂直于
且垂直于![]() 轴的直线被椭圆
轴的直线被椭圆![]() 截得的线段长为
截得的线段长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 过椭圆
过椭圆![]() 的右焦点
的右焦点![]() ,且与
,且与![]() 轴不重合,交椭圆
轴不重合,交椭圆![]() 于
于![]() 两点,过点
两点,过点![]() 且与
且与![]() 垂直的直线与圆
垂直的直线与圆![]() 交于
交于![]() 两点,求四边形
两点,求四边形![]() 面积的取值范围.
面积的取值范围.
参考答案:
【答案】(1)![]() (2)
(2)![]()
【解析】
试题分析:(1)过点![]() 且垂直于
且垂直于![]() 轴的直线被椭圆
轴的直线被椭圆![]() 截得的线段长为通径即
截得的线段长为通径即![]() ,而
,而![]() ,解方程组得
,解方程组得![]() (2)由于四边形对角线相互垂直,所以四边形
(2)由于四边形对角线相互垂直,所以四边形![]() 面积
面积![]() ,其中
,其中![]() 为直线与圆的弦长,可根据圆中垂径定理
为直线与圆的弦长,可根据圆中垂径定理![]() 求解,而
求解,而![]() 为直线与椭圆的弦长,可根据弦长公式求解
为直线与椭圆的弦长,可根据弦长公式求解![]() ,先讨论斜率不存在的情形
,先讨论斜率不存在的情形![]() ,
,![]() ,再考虑斜率存在情形:设
,再考虑斜率存在情形:设![]() 的方程
的方程![]() 联立方程组,结合韦达定理可得
联立方程组,结合韦达定理可得![]() ,根据点到直线距离公式可得
,根据点到直线距离公式可得![]() ,代入得
,代入得![]() ,综上可得四边形
,综上可得四边形![]() 面积的取值范围为
面积的取值范围为![]() .
.
试题解析:(1)由于![]() ,将
,将![]() 代入椭圆方程
代入椭圆方程![]() ,即
,即![]() ,由题意知
,由题意知![]() ,即
,即![]() ,又
,又![]() ,所以椭圆
,所以椭圆![]() 的方程
的方程![]() .
.
(2)当直线![]() 与
与![]() 轴不垂直时,设
轴不垂直时,设![]() 的方程
的方程![]() ,
,
由 ,得
,得![]() ,则
,则![]() ,
,
所以![]() ,过点
,过点![]() 且与
且与![]() 垂直的直线
垂直的直线![]() ,圆心
,圆心![]() 到
到![]() 的距离是
的距离是![]() ,所以
,所以 .
.
故四边形![]() 面积
面积![]() .可得当
.可得当![]() 与
与![]() 轴不垂直时,四边形
轴不垂直时,四边形![]() 面积的取值范围为
面积的取值范围为![]() .当
.当![]() 与
与![]() 轴垂直时,其方程为
轴垂直时,其方程为![]() ,四边形
,四边形![]() 面积为
面积为![]() ,综上,四边形
,综上,四边形![]() 面积的取值范围为
面积的取值范围为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
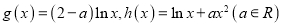 ,令
,令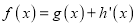 ,其中
,其中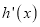 是函数
是函数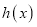 的导函数.
的导函数.(1)当
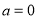 时,求
时,求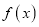 的极值;
的极值;(2)当
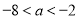 时,若存在
时,若存在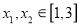 ,使得
,使得 恒成立,求
恒成立,求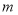 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为
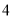 的菱形
的菱形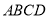 中,
中,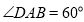 ,点
,点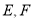 分别是边
分别是边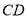 ,
,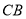 的中点,
的中点,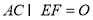 ,沿
,沿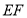 将
将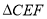 翻折到
翻折到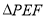 ,连接
,连接 ,得到如图的五棱锥
,得到如图的五棱锥 ,且
,且 .
.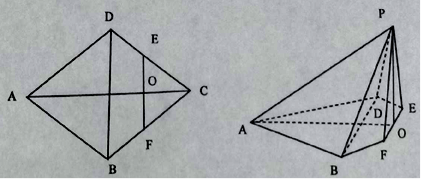
(1)求证:
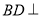 平面
平面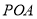 ;
;(2)求二面角
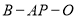 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义在
 上的函数
上的函数 是奇函数.
是奇函数.(1)求实数
 ,
, 的值;
的值;(2)判断
 的单调性,并用函数的单调性定义证明你的结论.
的单调性,并用函数的单调性定义证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】过棱柱不相邻两条侧棱的截面是 ( )
A. 矩形 B. 正方形
C. 梯形 D. 平行四边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知曲线
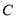 的方程是:
的方程是: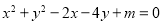 ,点
,点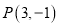 .
.(1)若
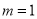 ,直线
,直线 过点
过点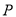 且与曲线
且与曲线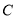 只有一个公共点,求直线
只有一个公共点,求直线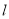 的方程;
的方程;(2)若曲线
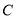 表示圆且被直线
表示圆且被直线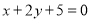 截得的弦长为
截得的弦长为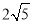 ,求实数
,求实数 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列四个命题:
①函数
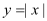 与函数
与函数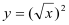 表示同一个函数;
表示同一个函数;②奇函数的图像一定通过直角坐标系的原点;
③函数
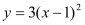 的图像可由
的图像可由 的图像向右平移1个单位得到;
的图像向右平移1个单位得到;④
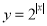 的最小值为1
的最小值为1⑤对于函数f(x),若f(-1)
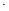 f(3)<0,则方程
f(3)<0,则方程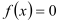 在区间[-1,3]上有一实根;
在区间[-1,3]上有一实根;其中正确命题的序号是 .(填上所有正确命题的序号)
相关试题

