【题目】自选题:已知曲线C1: ![]() (θ为参数),曲线C2:
(θ为参数),曲线C2: 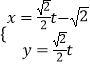 (t为参数).
(t为参数).
(1)指出C1 , C2各是什么曲线,并说明C1与C2公共点的个数;
(2)若把C1 , C2上各点的纵坐标都压缩为原来的一半,分别得到曲线C1′,C2′.写出C1′,C2′的参数方程.C1′与C2′公共点的个数和C与C2公共点的个数是否相同?说明你的理由.
参考答案:
【答案】
(1)解: C1是圆,C2是直线.C1的普通方程为x2+y2=1,
圆心C1(0,0),半径r=1.C2的普通方程为 ![]() .
.
因为圆心C1到直线 ![]() 的距离为1,
的距离为1,
所以C2与C1只有一个公共点.
(2)解:压缩后的参数方程分别为C1′: 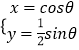 (θ为参数);
(θ为参数);
C2′: 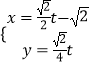 (t为参数).
(t为参数).
化为普通方程为:C1′:x2+4y2=1,C2′: ![]() ,
,
联立消元得 ![]() ,
,
其判别式 ![]() ,
,
所以压缩后的直线C2′与椭圆C1′仍然只有一个公共点,和C1与C2公共点个数相同
【解析】(1)先利用公式sin2θ+cos2θ=1将参数θ消去,得到圆的直角坐标方程,利用消元法消去参数t得到直线的普通方程,再根据圆心到直线的距离与半径进行比较,从而得到C1与C2公共点的个数;(2)求出压缩后的参数方程,再将参数方程化为普通方程,联立直线方程与圆的方程,利用判别式进行判定即可.
【考点精析】本题主要考查了直线的参数方程和圆的参数方程的相关知识点,需要掌握经过点![]() ,倾斜角为
,倾斜角为![]() 的直线
的直线![]() 的参数方程可表示为
的参数方程可表示为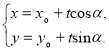 (
(![]() 为参数);圆
为参数);圆![]() 的参数方程可表示为
的参数方程可表示为![]() 才能正确解答此题.
才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,D,E分别为△ABC边AB,AC的中点,直线DE交△ABC的外接圆于F,G两点,若CF∥AB,证明:

(1)CD=BC;
(2)△BCD∽△GBD. -
科目: 来源: 题型:
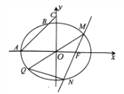
查看答案和解析>>【题目】已知椭圆
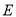 :
: 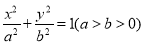 的左顶点为
的左顶点为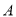 ,右焦点为
,右焦点为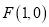 ,过点
,过点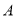 且斜率为1的直线交椭圆
且斜率为1的直线交椭圆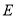 于另一点
于另一点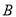 ,交
,交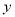 轴于点
轴于点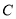 ,
, 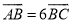 .
.
(1)求椭圆
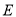 的方程;
的方程;(2)过点
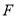 作直线
作直线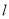 与椭圆
与椭圆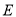 交于
交于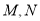 两点,连接
两点,连接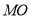 (
(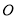 为坐标原点)并延长交椭圆
为坐标原点)并延长交椭圆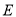 于点
于点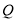 ,求
,求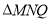 面积的最大值及取最大值时直线
面积的最大值及取最大值时直线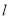 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
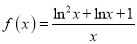 ,
, 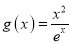 .
.(1)分别求函数
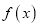 与
与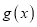 在区间
在区间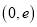 上的极值;
上的极值;(2)求证:对任意
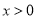 ,
, 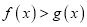 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】“微信运动”已成为当下热门的健身方式,小王的微信朋友圈内也有大量好友参与了“微信运动”,他随机选取了其中的40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下:
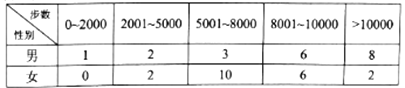
(1)若采用样本估计总体的方式,试估计小王的所有微信好友中每日走路步数超过5000步的概率;
(2)已知某人一天的走路步数超过8000步被系统评定“积极型”,否则为“懈怠型”,根据题意完成下面的
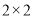 列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?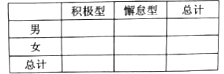 附:
附: 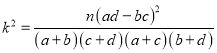 ,
,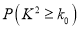
0.10
0.05
0.025
0.010
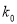
2.706
3.841
5.024
6.635
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=|x+a|+|x﹣2|
(1)当a=﹣3时,求不等式f(x)≥3的解集;
(2)若f(x)≤|x﹣4|的解集包含[1,2],求a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
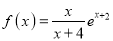 .
.(I)讨论函数的单调性,并证明当
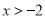 时,
时, 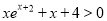 ;
;(Ⅱ)证明:当
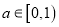 时,函数
时,函数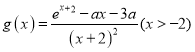 有最小值,设
有最小值,设 最小值为
最小值为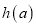 ,求函数
,求函数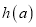 的值域.
的值域.
相关试题

