【题目】如图,D,E分别为△ABC边AB,AC的中点,直线DE交△ABC的外接圆于F,G两点,若CF∥AB,证明: 
(1)CD=BC;
(2)△BCD∽△GBD.
参考答案:
【答案】
(1)证明:∵D,E分别为△ABC边AB,AC的中点
∴DF∥BC,AD=DB
∵AB∥CF,∴四边形BDFC是平行四边形
∴CF∥BD,CF=BD
∴CF∥AD,CF=AD
∴四边形ADCF是平行四边形
∴AF=CD
∵ ![]() ,∴BC=AF,∴CD=BC
,∴BC=AF,∴CD=BC
(2)证明:由(1)知 ![]() ,所以
,所以 ![]() .
.
所以∠BGD=∠DBC.
因为GF∥BC,所以∠BDG=∠ADF=∠DBC=∠BDC.
所以△BCD~△GBD.
【解析】(1)根据D,E分别为△ABC边AB,AC的中点,可得DE∥BC,证明四边形ADCF是平行四边形,即可得到结论;(2)证明两组对应角相等,即可证得△BCD~△GBD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
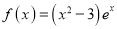 ,设关于
,设关于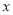 的方程
的方程 有
有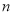 个不同的实数解,则
个不同的实数解,则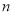 的所有可能的值为( )
的所有可能的值为( )A. 3 B. 1或3 C. 4或6 D. 3或4或6
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系
 中,直线
中,直线 的参数方程为
的参数方程为 (
( 为参数),以坐标原点
为参数),以坐标原点 为极点,以
为极点,以 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线 的极坐标方程为
的极坐标方程为 .
.(1)写出曲线
 的直角坐标方程;
的直角坐标方程;(2)已知点
 的直角坐标为
的直角坐标为 ,直线
,直线 与曲线
与曲线 相交于不同的两点
相交于不同的两点 ,求
,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=|ex﹣a|+|
 ﹣1|,其中a,x∈R,e是自然对数的底数,e=2.71828…
﹣1|,其中a,x∈R,e是自然对数的底数,e=2.71828…
(1)当a=0时,解不等式f(x)<2;
(2)求函数f(x)的单调增区间;
(3)设a≥ ,讨论关于x的方程f(f(x))=
,讨论关于x的方程f(f(x))=  的解的个数.
的解的个数. -
科目: 来源: 题型:
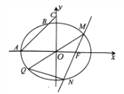
查看答案和解析>>【题目】已知椭圆
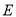 :
: 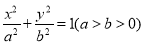 的左顶点为
的左顶点为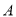 ,右焦点为
,右焦点为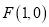 ,过点
,过点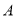 且斜率为1的直线交椭圆
且斜率为1的直线交椭圆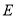 于另一点
于另一点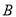 ,交
,交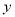 轴于点
轴于点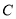 ,
, 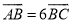 .
.
(1)求椭圆
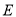 的方程;
的方程;(2)过点
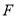 作直线
作直线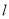 与椭圆
与椭圆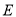 交于
交于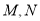 两点,连接
两点,连接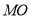 (
(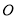 为坐标原点)并延长交椭圆
为坐标原点)并延长交椭圆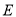 于点
于点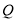 ,求
,求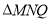 面积的最大值及取最大值时直线
面积的最大值及取最大值时直线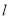 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
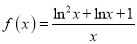 ,
, 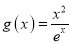 .
.(1)分别求函数
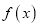 与
与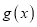 在区间
在区间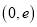 上的极值;
上的极值;(2)求证:对任意
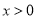 ,
, 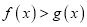 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】自选题:已知曲线C1:
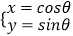 (θ为参数),曲线C2:
(θ为参数),曲线C2: 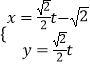 (t为参数).
(t为参数).
(1)指出C1 , C2各是什么曲线,并说明C1与C2公共点的个数;
(2)若把C1 , C2上各点的纵坐标都压缩为原来的一半,分别得到曲线C1′,C2′.写出C1′,C2′的参数方程.C1′与C2′公共点的个数和C与C2公共点的个数是否相同?说明你的理由.
相关试题

