【题目】已知椭圆![]() :
: ![]() 的左顶点为
的左顶点为![]() ,右焦点为
,右焦点为![]() ,过点
,过点![]() 且斜率为1的直线交椭圆
且斜率为1的直线交椭圆![]() 于另一点
于另一点![]() ,交
,交![]() 轴于点
轴于点![]() ,
, ![]() .
.
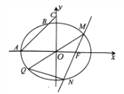
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作直线
作直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,连接
两点,连接![]() (
(![]() 为坐标原点)并延长交椭圆
为坐标原点)并延长交椭圆![]() 于点
于点![]() ,求
,求![]() 面积的最大值及取最大值时直线
面积的最大值及取最大值时直线![]() 的方程.
的方程.
参考答案:
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ) ![]() 面积的最大值为3,此时直线
面积的最大值为3,此时直线![]() 的方程为
的方程为![]()
【解析】试题分析:(1)根据题意列出关于![]() 、
、![]() 、
、![]() 的方程组,结合性质
的方程组,结合性质![]() ,
, ![]() ,求出
,求出![]() 、
、![]() 、
、![]() ,即可得结果;(2)设直线方程,代入椭圆方程,由韦达定理,弦长公式及基本不等式的性质,即可求得
,即可得结果;(2)设直线方程,代入椭圆方程,由韦达定理,弦长公式及基本不等式的性质,即可求得![]() 面积为
面积为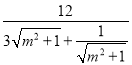 ,根据基本不等式可求最大值及直线
,根据基本不等式可求最大值及直线![]() 的方程.
的方程.
试题解析:(1)由题知![]() ,故
,故![]() ,代入椭圆
,代入椭圆![]() 的方程得
的方程得![]() ,又
,又![]() ,故
,故![]() ,椭圆
,椭圆![]() .
.
(2)由题知,直线![]() 不与
不与![]() 轴重合,故可设
轴重合,故可设![]() ,由
,由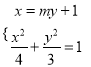 得
得![]() ,
,
设![]() ,则
,则![]() ,由
,由![]() 与
与![]() 关于原点对称知,
关于原点对称知,
![]()
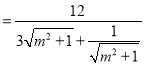 ,
,
![]() ,
, ![]() ,即
,即![]() ,当且仅当
,当且仅当![]() 时等号成立,
时等号成立,
![]() 面积的最大值为3,此时直线
面积的最大值为3,此时直线![]() 的方程为
的方程为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系
 中,直线
中,直线 的参数方程为
的参数方程为 (
( 为参数),以坐标原点
为参数),以坐标原点 为极点,以
为极点,以 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线 的极坐标方程为
的极坐标方程为 .
.(1)写出曲线
 的直角坐标方程;
的直角坐标方程;(2)已知点
 的直角坐标为
的直角坐标为 ,直线
,直线 与曲线
与曲线 相交于不同的两点
相交于不同的两点 ,求
,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=|ex﹣a|+|
 ﹣1|,其中a,x∈R,e是自然对数的底数,e=2.71828…
﹣1|,其中a,x∈R,e是自然对数的底数,e=2.71828…
(1)当a=0时,解不等式f(x)<2;
(2)求函数f(x)的单调增区间;
(3)设a≥ ,讨论关于x的方程f(f(x))=
,讨论关于x的方程f(f(x))=  的解的个数.
的解的个数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,D,E分别为△ABC边AB,AC的中点,直线DE交△ABC的外接圆于F,G两点,若CF∥AB,证明:

(1)CD=BC;
(2)△BCD∽△GBD. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
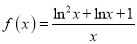 ,
, 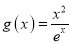 .
.(1)分别求函数
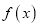 与
与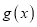 在区间
在区间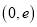 上的极值;
上的极值;(2)求证:对任意
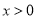 ,
, 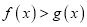 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】自选题:已知曲线C1:
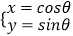 (θ为参数),曲线C2:
(θ为参数),曲线C2: 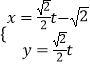 (t为参数).
(t为参数).
(1)指出C1 , C2各是什么曲线,并说明C1与C2公共点的个数;
(2)若把C1 , C2上各点的纵坐标都压缩为原来的一半,分别得到曲线C1′,C2′.写出C1′,C2′的参数方程.C1′与C2′公共点的个数和C与C2公共点的个数是否相同?说明你的理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】“微信运动”已成为当下热门的健身方式,小王的微信朋友圈内也有大量好友参与了“微信运动”,他随机选取了其中的40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下:
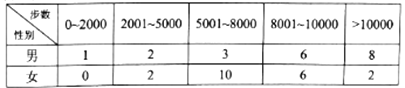
(1)若采用样本估计总体的方式,试估计小王的所有微信好友中每日走路步数超过5000步的概率;
(2)已知某人一天的走路步数超过8000步被系统评定“积极型”,否则为“懈怠型”,根据题意完成下面的
 列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?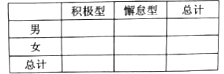 附:
附: 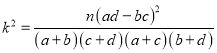 ,
,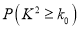
0.10
0.05
0.025
0.010
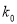
2.706
3.841
5.024
6.635
相关试题

