【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的最小值;
上的最小值;
(2)若![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(3)若![]() ,不等式
,不等式 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3) .
.
【解析】
试题分析:(1)由![]() 时,得出
时,得出![]() ,则
,则![]() ,再求导
,再求导![]() ,可得函数
,可得函数![]() 在
在![]() 上是增函数,从而得到函数
上是增函数,从而得到函数![]() 的单调性,即可求解函数
的单调性,即可求解函数![]() 在
在![]() 上的最小值; (2)由(1)知函数
上的最小值; (2)由(1)知函数![]() 在
在![]() 上是增函数,且
上是增函数,且![]() ,使得
,使得![]() ,得
,得![]() ,即
,即![]() ,设
,设![]() ,利用函数
,利用函数![]() 的单调性,即可求解求
的单调性,即可求解求![]() 的取值范围;(3)根据题意,转化为
的取值范围;(3)根据题意,转化为 对任意
对任意![]() 成立,令
成立,令 ,所以
,所以![]() ,可得出
,可得出![]() 的单调性,求解出
的单调性,求解出![]() 的最小值,即可
的最小值,即可![]() 的取值范围.
的取值范围.
试题解析:(1)![]() 时,
时,![]() ,
,![]() ,
,
![]() ,所以函数
,所以函数![]() 在
在![]() 上是增函数,
上是增函数,
又函数![]() 的值域为R,
的值域为R,
故![]() ,使得
,使得![]() ,
,
又![]() ,
,![]() ,所以当
,所以当![]() 时,
时,![]() ,
,
即函数![]() 在区间
在区间![]() 上递增,所以
上递增,所以![]()
(2)![]() ,
,
由(1)知函数![]() 在
在![]() 上是增函数,且
上是增函数,且![]() ,使得
,使得![]()
进而函数![]() 在区间
在区间![]() 上递减,在
上递减,在![]() 上递增,
上递增,
由![]() 得:
得:![]() ,
,
![]() ,
,![]() ,
,
因为![]() ,不等式
,不等式![]() 恒成立,
恒成立,
![]()
![]()
(另解:因为![]() ,不等式
,不等式![]() 恒成立,
恒成立,
即![]()
由![]() ,
,
当![]() 时取等号,
时取等号,![]() )
)
(3)由 ,
,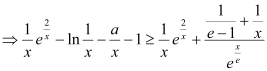 ,
,
 ,
, 对任意
对任意![]() 成立,
成立,
令函数 ,所以
,所以 ,
,
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以当![]() 时,函数
时,函数![]() 取得最小值
取得最小值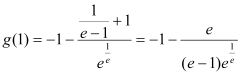 ,
,

-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标平面内,以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,已知点M的极坐标为
 ,曲线C的参数方程为
,曲线C的参数方程为 (α为参数).
(α为参数).(I)求直线OM的直角坐标方程;
(Ⅱ)求点M到曲线C上的点的距离的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某珠宝店的一件珠宝被盗,找到了甲、乙、丙、丁4个嫌疑人进行调查.甲说:“我没有偷”;乙说:“丙是小偷”;丙说:“丁是小偷”;丁说:“我没有偷”,若以上4人中只有一人说了真话,只有一人偷了珠宝,那么偷珠宝的人是_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从一箱产品中随机地抽取一件,设事件A=“抽到一等品”,事件B = “抽到二等品”,事件C =“抽到三等品”,且已知 P(A)= 0.65 ,P(B)=0.2 ,P(C)=0.1。则事件“抽到的不是一等品”的概率为( )
A. 0.65 B. 0.35 C. 0.3 D. 0.005
-
科目: 来源: 题型:
查看答案和解析>>【题目】“金导电、银导电、铜导电、锡导电,所以一切金属都导电”.此推理方法是( )
A. 完全归纳推理 B. 归纳推理 C. 类比推理 D. 演绎推理
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知曲线C1的极坐标方程为ρ2cos2θ=8,曲线C2的极坐标方程为
 ,曲线C1、C2相交于A、B两点.(p∈R)
,曲线C1、C2相交于A、B两点.(p∈R)(Ⅰ)求A、B两点的极坐标;
(Ⅱ)曲线C1与直线
 (t为参数)分别相交于M,N两点,求线段MN的长度.
(t为参数)分别相交于M,N两点,求线段MN的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(Ⅰ)当
 时,证明:
时,证明: ;
;(Ⅱ)当
 时,
时,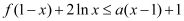 恒成立,求正实数
恒成立,求正实数 的值.
的值.
相关试题

