【题目】在直角坐标平面内,以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,已知点M的极坐标为![]() ,曲线C的参数方程为
,曲线C的参数方程为![]() (α为参数).
(α为参数).
(I)求直线OM的直角坐标方程;
(Ⅱ)求点M到曲线C上的点的距离的最小值.
参考答案:
【答案】(I)y=x(Ⅱ)![]()
【解析】
试题分析:(Ⅰ)利用x=ρcosθ,y=ρsinθ即可把点M的坐标化为直角坐标,进而即可求出直线OM的方程;(Ⅱ)把曲线C的参数方程化为化为普通方程,再利用|MA|-r即可求出最小值
试题解析:(Ⅰ)由点M的极坐标为![]() ,得点M的直角坐标
,得点M的直角坐标![]() ,
,![]() ,即M(4,4).
,即M(4,4).
∴直线OM的直角坐标方程为y=x.
(Ⅱ)由曲线C的参数方程![]() (α为参数),消去参数α得普通方程为:
(α为参数),消去参数α得普通方程为:
(x﹣1)2+y2=2.
∴圆心为A(1,0),半径![]() ,
,
由于点M在曲线C外,
故点M到曲线C上的点的距离的最小值为|MA|﹣r=![]()
![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】《论语·子路》篇中说:“名不正,则言不顺;言不顺,则事不成;事不成,则礼乐不兴;礼乐不兴,则刑罚不中;刑罚不中,则民无所措手足”,所以,名不正,则民无所措手足.上述推理过程用的是( )
A. 类比推理 B. 归纳推理 C. 演绎推理 D. 合情推理
-
科目: 来源: 题型:
查看答案和解析>>【题目】 如果学生的成绩大于或等于60分,则输出“及格”,否则输出“不及格”.用程序框图表示这一算法过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,圆
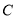 的方程为
的方程为 .以坐标原点
.以坐标原点 为极点,
为极点,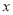 轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的单位长度,直线
轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的单位长度,直线 的极坐标方程
的极坐标方程 .
.(1)当
 时,判断直线
时,判断直线 与
与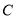 的关系;
的关系;(2)当
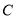 上有且只有一点到直线
上有且只有一点到直线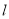 的距离等于
的距离等于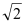 时,求
时,求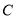 上到直线
上到直线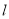 距离为
距离为 的点的坐标.
的点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】某珠宝店的一件珠宝被盗,找到了甲、乙、丙、丁4个嫌疑人进行调查.甲说:“我没有偷”;乙说:“丙是小偷”;丙说:“丁是小偷”;丁说:“我没有偷”,若以上4人中只有一人说了真话,只有一人偷了珠宝,那么偷珠宝的人是_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从一箱产品中随机地抽取一件,设事件A=“抽到一等品”,事件B = “抽到二等品”,事件C =“抽到三等品”,且已知 P(A)= 0.65 ,P(B)=0.2 ,P(C)=0.1。则事件“抽到的不是一等品”的概率为( )
A. 0.65 B. 0.35 C. 0.3 D. 0.005
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)当
 时,求函数
时,求函数 在
在 上的最小值;
上的最小值;(2)若
 ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围;
的取值范围;(3)若
 ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围.
的取值范围.
相关试题

