【题目】一片成熟森林的总面积为![]() (近期内不再种植),计划每年砍伐一些树,且每年砍伐面积的百分比相等,当砍伐到面积的一半时,所用时间是10年,为保护生态环境,森林面积至少要保留原面积的
(近期内不再种植),计划每年砍伐一些树,且每年砍伐面积的百分比相等,当砍伐到面积的一半时,所用时间是10年,为保护生态环境,森林面积至少要保留原面积的![]() ,已知到今年为止,森林剩余面积为原来的
,已知到今年为止,森林剩余面积为原来的![]() .
.
(1)求每年砍伐面积的百分比;
(2)到今年为止,该森林已砍伐了多少年?
(3)今后最多还能砍伐多少年?
参考答案:
【答案】(1)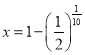 ;(2)砍伐了 5年;(3)今后最多还能砍伐15年.
;(2)砍伐了 5年;(3)今后最多还能砍伐15年.
【解析】试题分析:
(1)设每年砍伐面积的百分比为![]() ,由题意及指数函数的知识得
,由题意及指数函数的知识得![]()
![]() ,解得
,解得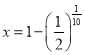 ,即为所求。(2)设经过
,即为所求。(2)设经过![]() 年剩余面积为原来的
年剩余面积为原来的![]() ,可得方程
,可得方程![]() ,解得
,解得![]() 。(3)设从今年开始,以后砍了
。(3)设从今年开始,以后砍了![]() 年,则
年,则![]() 年后剩余面积为
年后剩余面积为![]() .由
.由![]() ,化简得
,化简得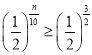 ,解得
,解得![]() ,即今后最多还能砍伐15年,由此可得结论。
,即今后最多还能砍伐15年,由此可得结论。
试题解析:
(1)设每年砍伐面积的百分比为![]() ,
,
则![]() ,即
,即![]() ,
,
解得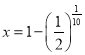 .
.
(2)设经过![]() 年剩余面积为原来的
年剩余面积为原来的![]() ,
,
由题意可得![]() ,
,
由(1)得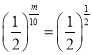 ,即
,即![]() ,
,
解得![]() ,
,
故到今年为止,已砍伐了 5年.
(3)设从今年开始,以后砍了![]() 年,则
年,则![]() 年后剩余面积为
年后剩余面积为![]() .
.
令![]() ,
,
即![]() ,
,
化简得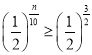 ,可得
,可得![]() ,
,
解得![]() .
.
故今后最多还能砍伐15年.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,正方体
 的棱长为1,
的棱长为1, 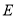 ,
, 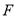 分别是棱
分别是棱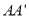 ,
, 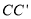 的中点,过直线
的中点,过直线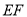 的平面分别与棱
的平面分别与棱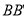 ,
, 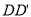 交于
交于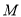 ,
, 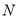 ,设
,设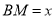 ,
, 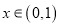 ,给出以下命题:
,给出以下命题:①四边形
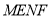 为平行四边形;
为平行四边形;②若四边形
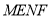 面积
面积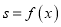 ,
, 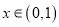 ,则
,则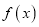 有最小值;
有最小值;③若四棱锥
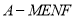 的体积
的体积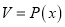 ,
, 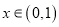 ,则
,则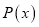 为常函数;
为常函数;④若多面体
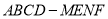 的体积
的体积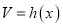 ,
, 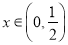 ,则
,则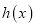 为单调函数.
为单调函数.⑤当
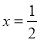 时,四边形
时,四边形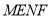 为正方形.
为正方形.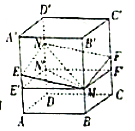
其中假命题的个数为( )
A. 0 B. 3 C. 2 D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为调查高三年级学生的身高情况,按随机抽样的方法抽取80名学生,得到男生身高情况的频率分布直方图(图1)和女生身高情况的频率分布直方图(图2).已知图1中身高在170~175cm的男生人数有16人.

(1)根据频率分布直方图,完成下列的
 列联表,并判断能有多大(百分几)的把握认为“身高与性别有关”?
列联表,并判断能有多大(百分几)的把握认为“身高与性别有关”?

总计
男生身高
女神身高
总计
(2)在上述80名学生中,从身高在170-175cm之间的学生按男、女性别分层抽样的方法,抽出5人,从这5人中选派3人当旗手,求3人中恰好有一名女生的概率.
参考公式:

参考数据:

0.025
0.610
0.005
0.001

5.024
4.635
7.879
10.828
-
科目: 来源: 题型:
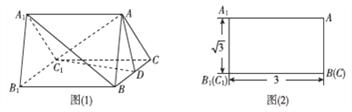
查看答案和解析>>【题目】如图(1)是一个水平放置的正三棱柱
 ,
,  是棱
是棱 的中点,正三棱柱的主视图如图(2).
的中点,正三棱柱的主视图如图(2).(1)图(1)中垂直于平面
 的平面有哪几个(直接写出符合要求的平面即可,不必说明或证明)
的平面有哪几个(直接写出符合要求的平面即可,不必说明或证明)(2)求正三棱柱
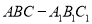 的体积;
的体积;(3)证明:
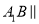 平面
平面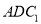 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】过椭圆
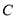 :
: 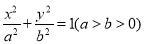 上一点
上一点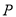 向
向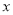 轴作垂线,垂足为右焦点
轴作垂线,垂足为右焦点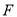 ,
, 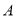 、
、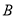 分别为椭圆
分别为椭圆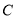 的左顶点和上顶点,且
的左顶点和上顶点,且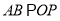 ,
, 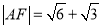 .
.(Ⅰ)求椭圆
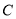 的方程;
的方程;(Ⅱ)若动直线
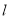 与椭圆
与椭圆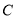 交于
交于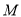 、
、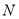 两点,且以
两点,且以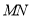 为直径的圆恒过坐标原点
为直径的圆恒过坐标原点 .问是否存在一个定圆与动直线
.问是否存在一个定圆与动直线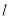 总相切.若存在,求出该定圆的方程;若不存在,请说明理由.
总相切.若存在,求出该定圆的方程;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
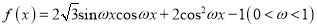 ,直线
,直线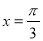 是函数
是函数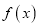 图象的一条对称轴.
图象的一条对称轴.(1)求
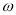 的值,并求
的值,并求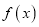 的解析式;
的解析式;(2)若关于
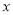 的方程
的方程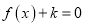 在区间
在区间 上有且只有一个实数解,求实数
上有且只有一个实数解,求实数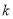 的取值范围;
的取值范围;(3)已知函数
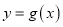 的图象是由
的图象是由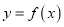 图象上的所有点的横坐标伸长到原来的2倍,然后再向左平移
图象上的所有点的横坐标伸长到原来的2倍,然后再向左平移 个单位得到,若
个单位得到,若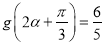 ,
, 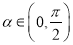 ,求
,求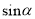 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】四名同学根据各自的样本数据研究变量
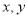 之间的相关关系,并求得回归直线方程和相关系数
之间的相关关系,并求得回归直线方程和相关系数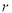 ,分别得到以下四个结论:
,分别得到以下四个结论: ①
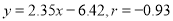 ②
②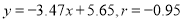
③
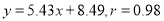 ④
④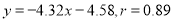
其中,一定不正确的结论序号是( )
A. ②③ B. ①④ C. ①②③ D. ②③④
相关试题

