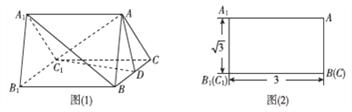
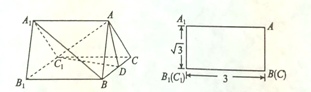
【题目】如图(1)是一个水平放置的正三棱柱![]() ,
, ![]() 是棱
是棱![]() 的中点,正三棱柱的主视图如图(2).
的中点,正三棱柱的主视图如图(2).
(1)图(1)中垂直于平面![]() 的平面有哪几个(直接写出符合要求的平面即可,不必说明或证明)
的平面有哪几个(直接写出符合要求的平面即可,不必说明或证明)
(2)求正三棱柱![]() 的体积;
的体积;
(3)证明: ![]() 平面
平面![]() .
.
参考答案:
【答案】(1)详见解析;(2)![]() ;(3)详见解析.
;(3)详见解析.
【解析】试题分析:(1)由于几何体为正三棱柱,故两个底面和侧面垂直,由于![]() 平面
平面![]() ,所以面
,所以面![]() 也和平面
也和平面![]() 垂直.(2)先计算得底面边长为
垂直.(2)先计算得底面边长为![]() ,由三视图可知高为
,由三视图可知高为![]() ,由此求得几何体的体积.(3)连接
,由此求得几何体的体积.(3)连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,利用三角形的中位线证明
,利用三角形的中位线证明![]() ,从而证明线面平行.
,从而证明线面平行.
试题解析:
(1)平面![]() 、平面
、平面![]() 、平面
、平面![]()
(2)依题意,在正三棱柱中, ![]() 从而
从而![]() .
.
所以正三棱柱的体积![]() .
.
(3)连接![]() 设
设![]() 连接
连接![]() .
.
因为![]() 是正三棱柱的侧面,所以
是正三棱柱的侧面,所以![]() 是矩形,
是矩形, ![]() 是
是![]() 的中点.
的中点.
所以![]() 是
是![]() 的中位线,
的中位线, ![]()
因为![]() 平面
平面![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】“共享单车”的出现,为我们提供了一种新型的交通方式.某机构为了调查人们对此种交通方式的满意度,从交通拥堵不严重的
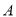 城市和交通拥堵严重的
城市和交通拥堵严重的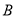 城市分别随机调查了20个用户,得到了一个用户满意度评分的样本,并绘制出茎叶图如图:
城市分别随机调查了20个用户,得到了一个用户满意度评分的样本,并绘制出茎叶图如图: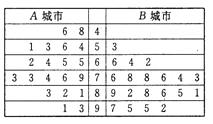
(Ⅰ)根据茎叶图,比较两城市满意度评分的平均值的大小及方差的大小(不要求具体解答过程,给出结论即可);
(Ⅱ)若得分不低于80分,则认为该用户对此种交通方式“认可”,否则认为该用户对此种交通方式“不认同”,请根据此样本完成此列联表,并局此样本分析是否有95%的把握认为城市拥堵与认可共享单车有关;
(Ⅲ)若此样本中的
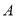 城市和
城市和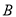 城市各抽取1人,则在此2人中恰有一人认可的条件下,此人来自
城市各抽取1人,则在此2人中恰有一人认可的条件下,此人来自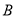 城市的概率是多少?
城市的概率是多少?

合计
认可
不认可
合计
附:
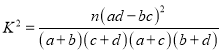
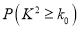
0.050
0.010
0.001
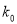
3.841
6.635
10.828
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,正方体
 的棱长为1,
的棱长为1, 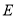 ,
, 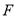 分别是棱
分别是棱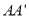 ,
, 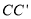 的中点,过直线
的中点,过直线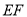 的平面分别与棱
的平面分别与棱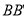 ,
, 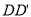 交于
交于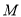 ,
, 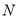 ,设
,设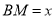 ,
, 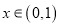 ,给出以下命题:
,给出以下命题:①四边形
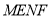 为平行四边形;
为平行四边形;②若四边形
 面积
面积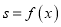 ,
, 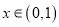 ,则
,则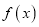 有最小值;
有最小值;③若四棱锥
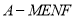 的体积
的体积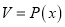 ,
, 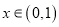 ,则
,则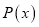 为常函数;
为常函数;④若多面体
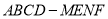 的体积
的体积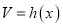 ,
, 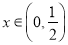 ,则
,则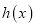 为单调函数.
为单调函数.⑤当
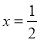 时,四边形
时,四边形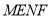 为正方形.
为正方形.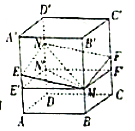
其中假命题的个数为( )
A. 0 B. 3 C. 2 D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为调查高三年级学生的身高情况,按随机抽样的方法抽取80名学生,得到男生身高情况的频率分布直方图(图1)和女生身高情况的频率分布直方图(图2).已知图1中身高在170~175cm的男生人数有16人.

(1)根据频率分布直方图,完成下列的
 列联表,并判断能有多大(百分几)的把握认为“身高与性别有关”?
列联表,并判断能有多大(百分几)的把握认为“身高与性别有关”?

总计
男生身高
女神身高
总计
(2)在上述80名学生中,从身高在170-175cm之间的学生按男、女性别分层抽样的方法,抽出5人,从这5人中选派3人当旗手,求3人中恰好有一名女生的概率.
参考公式:

参考数据:

0.025
0.610
0.005
0.001

5.024
4.635
7.879
10.828
-
科目: 来源: 题型:
查看答案和解析>>【题目】一片成熟森林的总面积为
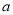 (近期内不再种植),计划每年砍伐一些树,且每年砍伐面积的百分比相等,当砍伐到面积的一半时,所用时间是10年,为保护生态环境,森林面积至少要保留原面积的
(近期内不再种植),计划每年砍伐一些树,且每年砍伐面积的百分比相等,当砍伐到面积的一半时,所用时间是10年,为保护生态环境,森林面积至少要保留原面积的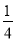 ,已知到今年为止,森林剩余面积为原来的
,已知到今年为止,森林剩余面积为原来的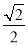 .
.(1)求每年砍伐面积的百分比;
(2)到今年为止,该森林已砍伐了多少年?
(3)今后最多还能砍伐多少年?
-
科目: 来源: 题型:
查看答案和解析>>【题目】过椭圆
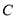 :
: 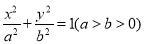 上一点
上一点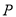 向
向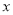 轴作垂线,垂足为右焦点
轴作垂线,垂足为右焦点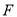 ,
, 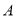 、
、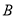 分别为椭圆
分别为椭圆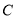 的左顶点和上顶点,且
的左顶点和上顶点,且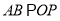 ,
, 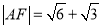 .
.(Ⅰ)求椭圆
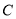 的方程;
的方程;(Ⅱ)若动直线
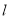 与椭圆
与椭圆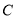 交于
交于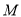 、
、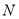 两点,且以
两点,且以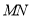 为直径的圆恒过坐标原点
为直径的圆恒过坐标原点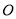 .问是否存在一个定圆与动直线
.问是否存在一个定圆与动直线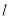 总相切.若存在,求出该定圆的方程;若不存在,请说明理由.
总相切.若存在,求出该定圆的方程;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
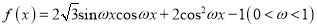 ,直线
,直线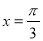 是函数
是函数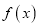 图象的一条对称轴.
图象的一条对称轴.(1)求
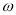 的值,并求
的值,并求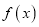 的解析式;
的解析式;(2)若关于
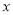 的方程
的方程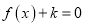 在区间
在区间 上有且只有一个实数解,求实数
上有且只有一个实数解,求实数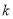 的取值范围;
的取值范围;(3)已知函数
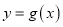 的图象是由
的图象是由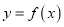 图象上的所有点的横坐标伸长到原来的2倍,然后再向左平移
图象上的所有点的横坐标伸长到原来的2倍,然后再向左平移 个单位得到,若
个单位得到,若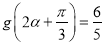 ,
, 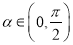 ,求
,求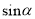 的值.
的值.
相关试题

