【题目】已知函数![]() 是定义域为
是定义域为![]() 的奇函数,当
的奇函数,当![]() .
.
(Ⅰ)求出函数![]() 在
在![]() 上的解析式;
上的解析式;
(Ⅱ)在答题卷上画出函数![]() 的图象,并根据图象写出
的图象,并根据图象写出![]() 的单调区间;
的单调区间;

(Ⅲ)若关于![]() 的方程
的方程![]() 有三个不同的解,求
有三个不同的解,求![]() 的取值范围。
的取值范围。
参考答案:
【答案】(Ⅰ)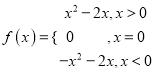 ;(Ⅱ)单调增区间为
;(Ⅱ)单调增区间为![]() ,
,
单调减区间为![]() ;(Ⅲ)
;(Ⅲ) ![]() .
.
【解析】试题分析; (Ⅰ)①由于函数![]() 是定义域为
是定义域为![]() 的奇函数,则
的奇函数,则![]() ;
;
②当![]() 时,
时, ![]() ,因为
,因为![]() 是奇函数,所以
是奇函数,所以![]() ,可得当
,可得当![]() 时
时![]() 的解析式,从而得到
的解析式,从而得到![]() 在
在![]() 上的解析式;
上的解析式;
(Ⅱ)根据(Ⅰ)得到的解析式可画出函数![]() 的图象,进而得到
的图象,进而得到![]() 的单调区间;
的单调区间;
(Ⅲ)由(1)可得![]() 有极大值1,极小值-1,进而可构造关于
有极大值1,极小值-1,进而可构造关于![]() 的不等式,解不等式可得答案.
的不等式,解不等式可得答案.
试题分析;(Ⅰ)①由于函数![]() 是定义域为
是定义域为![]() 的奇函数,则
的奇函数,则![]() ;
;
②当![]() 时,
时, ![]() ,因为
,因为![]() 是奇函数,所以
是奇函数,所以![]() .
.
所以![]() .
.
综上: 
(Ⅱ)图象如图所示.(图像给2分)
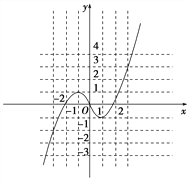
单调增区间: ![]()
单调减区间: ![]()
(Ⅲ)∵方程![]() 有三个不同的解
有三个不同的解
∴![]()
∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
 的前
的前 项和为
项和为 ,且满足
,且满足 ,求数列
,求数列 的通项公式.勤于思考的小红设计了下面两种解题思路,请你选择其中一种并将其补充完整.
的通项公式.勤于思考的小红设计了下面两种解题思路,请你选择其中一种并将其补充完整.思路1:先设
 的值为1,根据已知条件,计算出
的值为1,根据已知条件,计算出 _________,
_________,  __________,
__________,  _________.
_________.猜想:
 _______.
_______.然后用数学归纳法证明.证明过程如下:
①当
 时,________________,猜想成立
时,________________,猜想成立②假设
 (
( N*)时,猜想成立,即
N*)时,猜想成立,即 _______.
_______.那么,当
 时,由已知
时,由已知 ,得
,得 _________.
_________.又
 ,两式相减并化简,得
,两式相减并化简,得 _____________(用含
_____________(用含 的代数式表示).
的代数式表示).所以,当
 时,猜想也成立.
时,猜想也成立.根据①和②,可知猜想对任何
 N*都成立.
N*都成立.思路2:先设
 的值为1,根据已知条件,计算出
的值为1,根据已知条件,计算出 _____________.
_____________.由已知
 ,写出
,写出 与
与 的关系式:
的关系式:  _____________________,
_____________________,两式相减,得
 与
与 的递推关系式:
的递推关系式:  ____________________.
____________________.整理:
 ____________.
____________.发现:数列
 是首项为________,公比为_______的等比数列.
是首项为________,公比为_______的等比数列.得出:数列
 的通项公式
的通项公式 ____,进而得到
____,进而得到 ____________.
____________. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
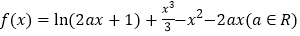 .
.(1)若
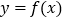 在
在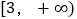 上为增函数,求实数
上为增函数,求实数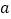 的取值范围;
的取值范围;(2)当
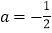 时,函数
时,函数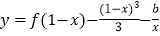 有零点,求实数
有零点,求实数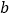 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】我国古代数学家刘徽是公元三世纪世界上最杰出的数学家,他在《九章算术圆田术》注中,用割圆术证明了圆面积的精确公式,并给出了计算圆周率的科学方法.所谓“割圆术”,即通过圆内接正多边形细割圆,并使正多边形的周长无限接近圆的周长,进而来求得较为精确的圆周率(圆周率指圆周长与该圆直径的比率).刘徽计算圆周率是从正六边形开始的,易知圆的内接正六边形可分为六个全等的正三角形,每个三角形的边长均为圆的半径
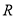
,此时圆内接正六边形的周长为

,此时若将圆内接正六边形的周长等同于圆的周长,可得圆周率为3,当用正二十四边形内接于圆时,按照上述算法,可得圆周率为__________.(参考数据:
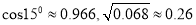
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
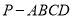 ,侧面
,侧面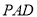 是边长为
是边长为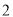 的正三角形,且与底面垂直,底面
的正三角形,且与底面垂直,底面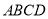 是
是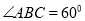 的菱形,
的菱形, 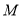 为
为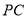 的中点.
的中点.(1)求证:
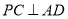 ;
;(2)求点
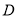 到平面
到平面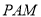 的距离.
的距离.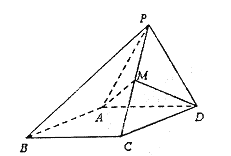
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016·桂林高二检测)如图所示,在四边形ABCD中,AB=AD=CD=1,BD=
 ,BD⊥CD,将四边形ABCD沿对角线BD折成四面体A′-BCD,使平面A′BD⊥平面BCD,则下列结论正确的是________.
,BD⊥CD,将四边形ABCD沿对角线BD折成四面体A′-BCD,使平面A′BD⊥平面BCD,则下列结论正确的是________.
(1)A′C⊥BD.(2)∠BA′C=90°.
(3)CA′与平面A′BD所成的角为30°.
(4)四面体A′-BCD的体积为
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】对于函数
 ,若在定义域内存在实数
,若在定义域内存在实数 ,满足
,满足 ,则称为“局部奇函数”
,则称为“局部奇函数”(1)已知二次函数
 (
( 且
且 ),试判断
),试判断 是否为“局部奇函数”,并说明理由;
是否为“局部奇函数”,并说明理由;(2)若
 是定义在区间
是定义在区间 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数 的取值范围;
的取值范围;(3)若
 为定义域为
为定义域为 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数 的取值范围;
的取值范围;
相关试题

