【题目】对于函数![]() ,若在定义域内存在实数
,若在定义域内存在实数![]() ,满足
,满足![]() ,则称为“局部奇函数”
,则称为“局部奇函数”
(1)已知二次函数![]() (
(![]() 且
且![]() ),试判断
),试判断![]() 是否为“局部奇函数”,并说明理由;
是否为“局部奇函数”,并说明理由;
(2)若![]() 是定义在区间
是定义在区间![]() 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数![]() 的取值范围;
的取值范围;
(3)若![]() 为定义域为
为定义域为![]() 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数![]() 的取值范围;
的取值范围;
参考答案:
【答案】(1)详见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(1)根据条件中局部奇函数的定义,只需判断方程![]() 是否有解即可下结论;(2)
是否有解即可下结论;(2)
根据局部奇函数的定义,参变分离后可得到![]() 关于
关于![]() 的函数关系式,即可求解;(3)根据局部奇函数的定
的函数关系式,即可求解;(3)根据局部奇函数的定
义,可得到![]() ,
,![]() 满足的式子,换元后可将问题等价转化为二次函数的零点分布,即可求解.
满足的式子,换元后可将问题等价转化为二次函数的零点分布,即可求解.
试题解析:(1)由题意得:![]() ,当
,当![]() 或
或![]() 时,
时,
![]() 成立,∴
成立,∴![]() 是“局部奇函数”;(2)由题意得:
是“局部奇函数”;(2)由题意得:![]()
∵![]() ,∴
,∴![]() 在
在![]() 有解,∴
有解,∴![]() ,
,![]() ,
,
令![]() ,则
,则![]() ,设
,设![]() ,
,![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增,
单调递增,
∴![]() ,∴
,∴![]() ;(3)由定义得:∵
;(3)由定义得:∵![]() ,
,
∴![]() ,即
,即![]() 有解,
有解,
设![]() ,∴方程等价于
,∴方程等价于![]() 在
在![]() 时有解,
时有解,
设![]() ,对称轴
,对称轴![]() ,
,
①若![]() ,则
,则![]() ,即
,即![]() ,∴
,∴![]() ,
,
此时![]() ,②若
,②若![]() 时,则
时,则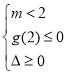 ,即
,即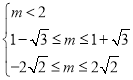 ,此时
,此时![]() ,
,
综上得:![]() ,即实数
,即实数![]() 的取值范围是
的取值范围是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 是定义域为
是定义域为 的奇函数,当
的奇函数,当 .
.(Ⅰ)求出函数
 在
在 上的解析式;
上的解析式;(Ⅱ)在答题卷上画出函数
 的图象,并根据图象写出
的图象,并根据图象写出 的单调区间;
的单调区间;
(Ⅲ)若关于
 的方程
的方程 有三个不同的解,求
有三个不同的解,求 的取值范围。
的取值范围。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
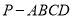 ,侧面
,侧面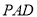 是边长为
是边长为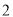 的正三角形,且与底面垂直,底面
的正三角形,且与底面垂直,底面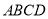 是
是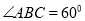 的菱形,
的菱形, 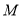 为
为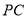 的中点.
的中点.(1)求证:
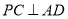 ;
;(2)求点
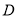 到平面
到平面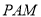 的距离.
的距离.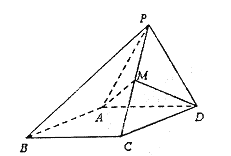
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016·桂林高二检测)如图所示,在四边形ABCD中,AB=AD=CD=1,BD=
 ,BD⊥CD,将四边形ABCD沿对角线BD折成四面体A′-BCD,使平面A′BD⊥平面BCD,则下列结论正确的是________.
,BD⊥CD,将四边形ABCD沿对角线BD折成四面体A′-BCD,使平面A′BD⊥平面BCD,则下列结论正确的是________.
(1)A′C⊥BD.(2)∠BA′C=90°.
(3)CA′与平面A′BD所成的角为30°.
(4)四面体A′-BCD的体积为
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知随机变量
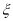 的取值为不大于
的取值为不大于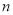 的非负整数值,它的分布列为:
的非负整数值,它的分布列为: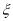
0
1
2
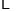
n
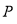
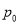
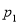
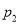
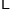
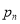
其中
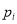 (
(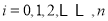 )满足:
)满足: 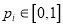 ,且
,且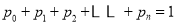 .
.定义由
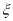 生成的函数
生成的函数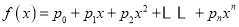 ,令
,令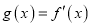 .
.(I)若由
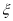 生成的函数
生成的函数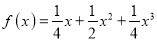 ,求
,求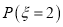 的值;
的值;(II)求证:随机变量
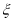 的数学期望
的数学期望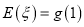 ,
, 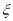 的方差
的方差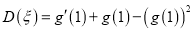 ;
;(
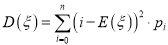 )
)(Ⅲ)现投掷一枚骰子两次,随机变量
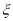 表示两次掷出的点数之和,此时由
表示两次掷出的点数之和,此时由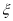 生成的函数记为
生成的函数记为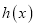 ,求
,求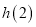 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分12分)某公司的广告费支出x与销售额y(单位:万元)之间有下列对应数据
x
2
4
5
6
8
y
30
40
60
50
70
(1)画出散点图,并判断广告费与销售额是否具有相关关系;
(2)根据表中提供的数据,用最小二乘法求出y与x的回归方程
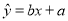 ;
;(3)预测销售额为115万元时,大约需要多少万元广告费。
参考公式:回归方程为
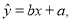 其中
其中 ,
, 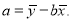
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
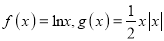
.
(1)求

在
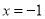
处的切线方程;
(2)令

,求

的单调区间;
(3)若任意

且

,都有
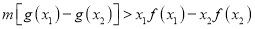
恒成立,求实数
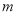
的取值范围.
相关试题

