【题目】已知焦点在![]() 轴上的椭圆
轴上的椭圆![]() 的中心是原点
的中心是原点![]() ,离心率为双曲线
,离心率为双曲线![]() 离心率的一半,直线
离心率的一半,直线![]() 被椭圆
被椭圆![]() 截得的线段长为
截得的线段长为![]() .直线
.直线![]() :
: ![]() 与
与![]() 轴交于点
轴交于点![]() ,与椭圆
,与椭圆![]() 交于
交于![]() 两个相异点,且
两个相异点,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)是否存在实数![]() ,使
,使![]() ?若存在,求
?若存在,求![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
参考答案:
【答案】(Ⅰ) ![]() ;(Ⅱ)
;(Ⅱ) ![]() 或
或![]() 或
或![]() .
.
【解析】试题分析:(Ⅰ)设出椭圆的标准方程,利用离心率、四边形的周长进行求解;(Ⅱ)利用平面向量的线性运算得到![]() 的关系,联立直线与椭圆的方程,得到关于
的关系,联立直线与椭圆的方程,得到关于![]() 的一元二次方程,利用椭圆的对称性、平面向量的坐标运算和判别式进行求解.
的一元二次方程,利用椭圆的对称性、平面向量的坐标运算和判别式进行求解.
试题解析:(Ⅰ)根据已知设椭圆![]() 的方程为
的方程为![]() ,焦距为
,焦距为![]() ,
,
由已知得![]() ,∴
,∴![]() .
.
∵以椭圆![]() 的长轴和短轴为对角线的四边形的周长为
的长轴和短轴为对角线的四边形的周长为![]() ,
,
∴![]() .
.
∴椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)根据已知得![]() ,由
,由![]() ,得
,得![]() .
.
∴![]() .∵
.∵![]() ,∴
,∴![]() ,
,
若![]() ,由椭圆的对称性得
,由椭圆的对称性得![]() ,即
,即![]() .
.
∴![]() 能使
能使![]() 成立.
成立.
若![]() ,则
,则![]() ,解得
,解得![]() .
.
设![]() ,由
,由![]() 得
得![]() ,
,
由已知得![]() ,即
,即![]() .
.
且![]() .…10分
.…10分
由![]() 得
得![]() ,即
,即![]() .∴
.∴![]() ,
,
∴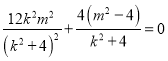 ,即
,即![]() .
.
当![]() 时,
时, ![]() 不成立.∴
不成立.∴![]() ,
,
∵![]() ,∴
,∴![]() ,即
,即![]() .
.
∴![]() ,解得
,解得![]() 或
或![]() .
.
综上述,当![]() 或
或![]() 或
或![]() 时,
时, ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 :
:  (
( )的焦距为
)的焦距为 ,点
,点 在
在 上.
上.(Ⅰ)求椭圆
 的方程;
的方程;(Ⅱ)设点
 在
在 上,点
上,点 的轨迹为曲线
的轨迹为曲线 ,过原点作直线
,过原点作直线 与曲线
与曲线 交于
交于 、
、 两点,点
两点,点 ,证明:
,证明:  为定值,并求出定值.
为定值,并求出定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在正方体ABCD-A1B1C1D1中,E为AB的中点,F为AA1的中点.求证:CE,D1F,DA三线交于一点.
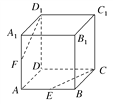
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题正确的是__________.(写出所有正确命题的序号)
①已知
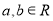 ,“
,“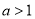 且
且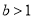 ”是“
”是“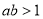 ”的充要条件;
”的充要条件;②已知平面向量
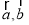 ,“
,“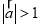 且
且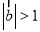 ”是“
”是“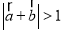 ”的必要不充分条件;
”的必要不充分条件;③已知
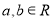 ,“
,“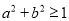 ”是“
”是“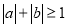 ”的充分不必要条件;
”的充分不必要条件;④命题
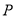 :“
:“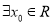 ,使
,使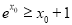 且
且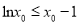 ”的否定为
”的否定为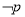 :“
:“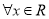 ,都有
,都有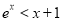 且
且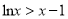 ”
” -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,正方体ABCD-A1B1C1D1中,M、N分别是A1B1、B1C1的中点,问:

(1)AM和CN是否是异面直线?说明理由;
(2)D1B和CC1是否是异面直线?说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在平面直角坐标系中,
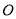 是坐标原点,动圆
是坐标原点,动圆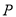 经过点
经过点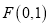 ,且与直线
,且与直线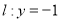 相切.
相切.(1)求动圆圆心
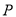 的轨迹方程
的轨迹方程 ;
;(2)过
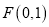 的直线
的直线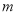 交曲线
交曲线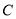 于
于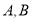 两点,过
两点,过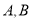 作曲线
作曲线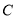 的切线
的切线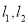 ,直线
,直线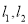 交于点
交于点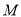 ,求
,求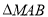 的面积的最小值.
的面积的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在哈尔滨的中央大街的步行街同侧有6块广告牌,牌的底色可选用红、蓝两种颜色,若要求相邻两块牌的底色不都为蓝色,则不同的配色方案共有( )
A. 20 B. 21 C. 22 D. 24
相关试题

