【题目】几个月前,成都街头开始兴起“mobike”、“ofo”等共享单车,这样的共享单车为很多市民解决了最后一公里的出行难题.然而,这种模式也遇到了一些让人尴尬的问题,比如乱停乱放,或将共享单车占为“私有”等.
为此,某机构就是否支持发展共享单车随机调查了50人,他们年龄的分布及支持发展共享单车的人数统计如下表:
年龄 |
|
|
|
|
|
|
受访人数 | 5 | 6 | 15 | 9 | 10 | 5 |
支持发展 共享单车人数 | 4 | 5 | 12 | 9 | 7 | 3 |
(Ⅰ)由以上统计数据填写下面的![]() 列联表,并判断能否在犯错误的概率不超过0.1的前提下,认为年龄与是否支持发展共享单车有关系;
列联表,并判断能否在犯错误的概率不超过0.1的前提下,认为年龄与是否支持发展共享单车有关系;
年龄低于35岁 | 年龄不低于35岁 | 合计 | |
支持 | |||
不支持 | |||
合计 |
(Ⅱ)若对年龄在![]() ,
,![]() 的被调查人中各随机选取两人进行调查,记选中的4人中支持发展共享单车的人数为
的被调查人中各随机选取两人进行调查,记选中的4人中支持发展共享单车的人数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:![]() ,其中
,其中![]() .
.
参考答案:
【答案】(Ⅰ)见解析;(Ⅱ)见解析.
【解析】试题分析:(1)由题意可知a=30,b=10,c=5,d=5,代入:![]() 。(2)
。(2)
年龄在![]() 的5个受访人中,有4人支持发展共享单车;年龄在
的5个受访人中,有4人支持发展共享单车;年龄在![]() 的6个受访人中,有5人支持发展共享单车.随机变量
的6个受访人中,有5人支持发展共享单车.随机变量![]() 的所有可能取值为2,3,4.所以
的所有可能取值为2,3,4.所以![]() ,
,![]() ,
,![]() .
.
试题解析:(Ⅰ)根据所给数据得到如下![]() 列联表:
列联表:
年龄低于35岁 | 年龄不低于35岁 | 合计 | |
支持 | 30 | 10 | 40 |
不支持 | 5 | 5 | 10 |
合计 | 35 | 15 | 50 |
根据![]() 列联表中的数据,得到
列联表中的数据,得到![]() 的观测值为
的观测值为
![]()
![]() .
.
∴不能在犯错误的概率不超过0.1的前提下,认为年龄与是否支持发展共享单车有关系.
(Ⅱ)由题意,年龄在![]() 的5个受访人中,有4人支持发展共享单车;年龄在
的5个受访人中,有4人支持发展共享单车;年龄在![]() 的6个受访人中,有5人支持发展共享单车.
的6个受访人中,有5人支持发展共享单车.
∴随机变量![]() 的所有可能取值为2,3,4.
的所有可能取值为2,3,4.
∵![]() ,
,![]() ,
,![]() ,
,
∴随机变量![]() 的分布列为
的分布列为
| 2 | 3 | 4 |
|
|
|
|
∴随机变量![]() 的数学期望
的数学期望![]() .
.
-
科目: 来源: 题型:
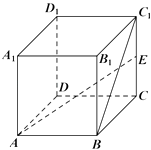
查看答案和解析>>【题目】长方体ABCD﹣A1B1C1D1中AB=AA1=2,AD=1,E为CC1的中点,则异面直线BC1与AE所成角的余弦值为( )
A.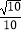
B.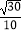
C.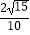
D.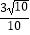
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x3﹣
 ax2 , 且关于x的方程f(x)+a=0有三个不等的实数根,则实数a的取值范围是( )
ax2 , 且关于x的方程f(x)+a=0有三个不等的实数根,则实数a的取值范围是( )
A.(﹣∞,﹣ )∪(0,
)∪(0,  )
)
B.(﹣ ,0)∪(
,0)∪(  ,+∞)
,+∞)
C.(﹣ ,
,  )
)
D.(﹣∞,﹣ )∪(
)∪(  ,+∞)
,+∞) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
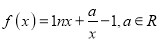 .
.(1)若关于
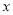 的不等式
的不等式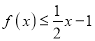 在
在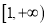 上恒成立,求
上恒成立,求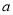 的取值范围;
的取值范围;(2)设函数
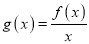 ,若
,若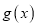 在
在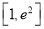 上有两个不同极值点,求
上有两个不同极值点,求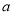 的取值范围,并判断极值的正负.
的取值范围,并判断极值的正负. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知k∈R,
 =(k,1),
=(k,1),  =(2,4),若|
=(2,4),若|  |<
|<  ,则△ABC是钝角三角形的概率是( )
,则△ABC是钝角三角形的概率是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知曲线
 的极坐标方程为
的极坐标方程为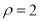 ,在以极点为直角坐标原点
,在以极点为直角坐标原点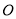 ,极轴为
,极轴为 轴的正半轴建立的平面直角坐标系
轴的正半轴建立的平面直角坐标系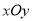 中,直线
中,直线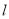 的参数方程为
的参数方程为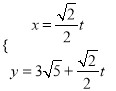 (
(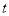 为参数).
为参数).(1)写出直线
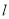 的普通方程与曲线
的普通方程与曲线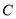 的直角坐标方程;
的直角坐标方程;(2)在平面直角坐标系中,设曲线
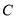 经过伸缩变换
经过伸缩变换 :
: 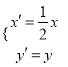 得到曲线
得到曲线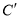 ,若
,若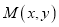 为曲线
为曲线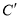 上任意一点,求点
上任意一点,求点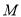 到直线
到直线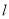 的最小距离.
的最小距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了检验学习情况,某培训机构于近期举办一场竞赛活动,分别从甲、乙两班各抽取10名学员的成绩进行统计分析,其成绩的茎叶图如图所示(单位:分),假设成绩不低于90分者命名为“优秀学员”.
(1)分别求甲、乙两班学员成绩的平均分(结果保留一位小数);
(2)从甲班4名优秀学员中抽取两人,从乙班2名80分以下的学员中抽取一人,求三人平均分不低于90分的概率.

相关试题

