【题目】甲乙两人进行两种游戏,两种游戏规则如下:游戏Ⅰ:口袋中有质地、大小完全相同的5个球,编号分别为1,2,3,4,5,甲先摸出一个球,记下编号,放回后乙再摸一个球,记下编号,如果两个编号的和为偶数算甲赢,否则算乙赢.游戏Ⅱ:口袋中有质地、大小完全相同的6个球,其中4个白球,2个红球,由裁判有放回的摸两次球,即第一次摸出记下颜色后放回再摸第二次,摸出两球同色算甲赢,摸出两球不同色算乙赢.
(Ⅰ)求游戏Ⅰ中甲赢的概率;
(Ⅱ)求游戏Ⅱ中乙赢的概率;并比较这两种游戏哪种游戏更公平?试说明理由.
参考答案:
【答案】解:(Ⅰ)∵游戏Ⅰ中有放回地依次摸出两球基本事件有5*5=25种,其中甲赢包含(1,1)(1,3)(1,5)(3,3)(3,5)(5,5)(3,1)(5,1)(5,3)(2,2)(2,4)(4,4)(4,2)13种基本事件,
∴游戏Ⅰ中甲赢的概率为:P= ![]()
(Ⅱ)设4个白球为a,b,c,d,2个红球为A,B,则游戏Ⅱ中有放回地依次摸出两球基本事件有6*6=36种,其中乙赢包含(a,A),(b,A),(c,A)(d,A)(a,B)(b,B)(c,B)(d,B)(A,a)(A,b)(A,c)(A,d)(B,a)(B,b)(B,c)(B,d)16种基本事件,
∴游戏Ⅱ中乙赢的概率为:P’= ![]()
∵ ![]() .∴游戏Ⅰ更公平
.∴游戏Ⅰ更公平
【解析】(Ⅰ)列出甲赢包含基本事件总数,所有基本事件数目,即可求解游戏Ⅰ中甲赢的概率.(Ⅱ)设4个白球为a,b,c,d,2个红球为A,B,则游戏Ⅱ中有放回地依次摸出两球基本事件有6*6=36种,其中乙赢包含16种基本事件,求出概率,即可判断游戏的公平程度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知命题p:x∈A,且A={x|a﹣1<x<a+1},命题q:x∈B,且B={x|x2﹣4x+3≥0}
(Ⅰ)若A∩B=,A∪B=R,求实数a的值;
(Ⅱ)若p是q的充分条件,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系
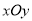 中,直线
中,直线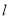 的参数方程为
的参数方程为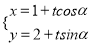 (
(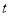 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系 取相同的长度单位,且以原点
取相同的长度单位,且以原点 为极点,以
为极点,以 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆 的方程为
的方程为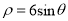 .
.(1)求圆
 的直角坐标方程;
的直角坐标方程;(2)设圆
 与直线
与直线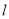 交于点
交于点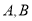 ,若点
,若点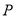 的坐标为
的坐标为 ,求
,求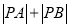 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆x2+4y2=4,直线l:y=x+m
(1)若l与椭圆有一个公共点,求m的值;
(2)若l与椭圆相交于P、Q两点,且|PQ|等于椭圆的短轴长,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】20名同学参加某次数学考试成绩(单位:分)的频率分布直方图如下:
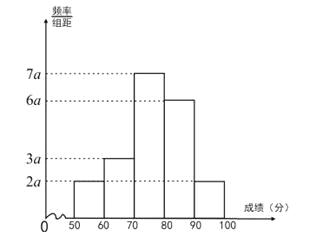
(Ⅰ)求频率分布直方图中
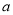 的值;
的值;(Ⅱ)分别求出成绩落在
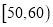 ,
, 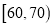 中的学生人数;
中的学生人数;(Ⅲ)从成绩在
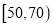 的学生中任选2人,求此2人的成绩都在
的学生中任选2人,求此2人的成绩都在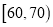 中的概率.
中的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】在三棱锥ABC﹣A1B1C1中,底面ABC是边长为2的正三角形,侧棱AA1⊥底面ABC,AA1=
 ,P、Q分别是AB、AC上的点,且PQ∥BC.
,P、Q分别是AB、AC上的点,且PQ∥BC. 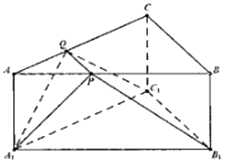
(1)若平面A1PQ与平面A1B1C1相交于直线l,求证:l∥B1C1;
(2)当平面A1PQ⊥平面PQC1B1时,确定点P的位置并说明理由.S. -
科目: 来源: 题型:
查看答案和解析>>【题目】设数列{an}的前n项和为Sn , 对任意的正整数n,都有an=5Sn+1成立,记bn=
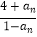 (n∈N*).
(n∈N*).
(1)求数列{an}和数列{bn}的通项公式;
(2)设数列{bn}的前n项和为Rn , 求证:对任意的n∈N* , 都有Rn<4n;
(3)记cn=b2n﹣b2n﹣1(n∈N*),设数列{cn}的前n项和为Tn , 求证:对任意n∈N* , 都有Tn< .
.
相关试题

