【题目】长春市的“名师云课”活动自开展以来获得广大家长和学生的高度赞誉,在我市推出的第二季名师云课中,数学学科共计推出36节云课,为了更好地将课程内容呈现给学生,现对某一时段云课的点击量进行统计:
点击量 |
|
|
|
节数 | 6 | 18 | 12 |
(Ⅰ)现从36节云课中采用分层抽样的方式选出6节,求选出的点击量超过3000的节数.
(Ⅱ)为了更好地搭建云课平台,现将云课进行剪辑,若点击量在区间![]() 内,则需要花费40分钟进行剪辑,若点击量在区间
内,则需要花费40分钟进行剪辑,若点击量在区间![]() 内,则需要花费20分钟进行剪辑,点击量超过3000,则不需要剪辑,现从(Ⅰ)中选出的6节课中随机取出2节课进行剪辑,求剪辑时间
内,则需要花费20分钟进行剪辑,点击量超过3000,则不需要剪辑,现从(Ⅰ)中选出的6节课中随机取出2节课进行剪辑,求剪辑时间![]() 的分布列与数学期望.
的分布列与数学期望.
参考答案:
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】试题分析:(Ⅰ)因为 36节云课中采用分层抽样的方式选出6节,所以![]() 节应选出
节应选出![]() 节;(Ⅱ)
节;(Ⅱ)![]() 的所有可能取值为
的所有可能取值为![]() ,根据古典概型概率公式分别求出各随机变量的概率,从而可得分布列,由期望公式可得结果..
,根据古典概型概率公式分别求出各随机变量的概率,从而可得分布列,由期望公式可得结果..
试题解析:(Ⅰ)根据分层抽样,选出的6节课中有2节点击量超过3000.
(Ⅱ)![]() 的可能取值为0,20,40,60
的可能取值为0,20,40,60
![]()
![]()
![]()
![]()
则![]() 的分布列为
的分布列为
| 0 | 20 | 40 | 60 |
|
|
|
|
|
即![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校高一年级的A,B,C三个班共有学生120人,为调查他们的体育锻炼情况,用分层抽样的方法从这三个班中分别抽取4,5,6名学生进行调查. (Ⅰ)求A,B,C三个班各有学生多少人;
(Ⅱ)记从C班抽取学生的编号依次为C1 , C2 , C3 , C4 , C5 , C6 , 现从这6名学生中随机抽取2名做进一步的数据分析.
(i)列出所有可能抽取的结果;
(ii)设A为事件“编号为C1和C2的2名学生中恰有一人被抽到”,求事件A发生的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}满足(an+1﹣1)(an﹣1)=3(an﹣an+1),a1=2,令
 .
.
(Ⅰ)证明:数列{bn}是等差数列;
(Ⅱ)求数列{an}的通项公式. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(0,﹣2),椭圆E:
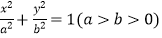 的离心率为
的离心率为 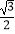 ,F是椭圆E的右焦点,直线AF的斜率为
,F是椭圆E的右焦点,直线AF的斜率为 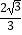 ,O为坐标原点.
,O为坐标原点.
(1)求椭圆E的方程;
(2)设过点A的动直线与椭圆E相交于P,Q两点,当△OPQ的面积最大时,求直线l的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前n项和Sn满足Sn=
 n2+
n2+  n(n∈N*),数列{bn}是首项为4的正项等比数列,且2b2 , b3﹣3,b2+2成等差数列. (Ⅰ)求数列{an},{bn}的通项公式;
n(n∈N*),数列{bn}是首项为4的正项等比数列,且2b2 , b3﹣3,b2+2成等差数列. (Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)令cn=anbn(n∈N*),求数列{cn}的前n项和Tn . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义在
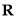 上的函数
上的函数 满足:函数
满足:函数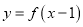 的图象关于直线
的图象关于直线 对称,且当
对称,且当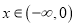 时
时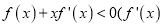 是函数
是函数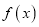 的导函数)成立.若
的导函数)成立.若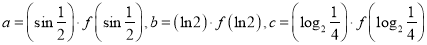 ,则
,则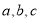 的大小关系是
的大小关系是A.
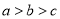 B.
B. 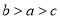 C.
C. 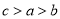 D.
D. 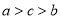
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
 是定义在
是定义在 上的奇函数,且对任意实数
上的奇函数,且对任意实数 ,恒有
,恒有 ,当
,当 时,
时, 
(1)求证:
 是周期函数;
是周期函数;(2)当
 时,求
时,求 的解析式;
的解析式;(3)计算

相关试题

