【题目】已知函数![]() (
(![]() ).
).
(1)若不等式![]() 的解集为
的解集为![]() ,求
,求![]() 的取值范围;
的取值范围;
(2)当![]() 时,解不等式
时,解不等式![]() ;
;
(3)若不等式![]() 的解集为
的解集为![]() ,若
,若![]() ,求
,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .;(3)
.;(3)![]() .
.
【解析】试题分析:(1)对二项式系数进行讨论,可得![]() 求出解集即可;(2)分为
求出解集即可;(2)分为![]() ,
, ![]() ,
, ![]() 分别解出3种情形对应的不等式即可;(3)将问题转化为对任意的
分别解出3种情形对应的不等式即可;(3)将问题转化为对任意的![]() ,不等式
,不等式![]() 恒成立,利用分离参数的思想得
恒成立,利用分离参数的思想得![]() 恒成立,求出其最大值即可.
恒成立,求出其最大值即可.
试题解析:(1)①当![]() 即
即![]() 时,
时, ![]() ,不合题意;
,不合题意;
②当![]() 即
即![]() 时,
时,
![]() ,即
,即![]() ,
,
∴ ,∴
,∴![]()
(2)![]() 即
即![]()
即![]()
①当![]() 即
即![]() 时,解集为
时,解集为![]()
②当![]() 即
即![]() 时,
时, ![]()
∵![]() ,∴解集为
,∴解集为![]()
③当![]() 即
即![]() 时,
时, ![]()
∵![]() ,所以
,所以![]() ,所以
,所以![]()
∴解集为![]()
(3)不等式![]() 的解集为
的解集为![]() ,
, ![]() ,
,
即对任意的![]() ,不等式
,不等式![]() 恒成立,
恒成立,
即![]() 恒成立,
恒成立,
因为![]() 恒成立,所以
恒成立,所以![]() 恒成立,
恒成立,
设![]() 则
则![]() ,
, ![]() ,
,
所以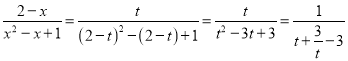 ,
,
因为![]() ,当且仅当
,当且仅当![]() 时取等号,
时取等号,
所以![]() ,当且仅当
,当且仅当![]() 时取等号,
时取等号,
所以当![]() 时,
时, 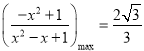 ,
,
所以![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
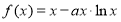 (
(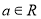 ).
).(1)当
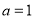 时,求函数
时,求函数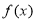 的单调区间;
的单调区间;(2)设
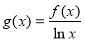 ,若函数
,若函数 在
在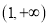 上为减函数,求实数
上为减函数,求实数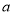 的最小值;
的最小值;(3)若存在
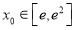 ,使得
,使得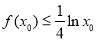 成立,求实数
成立,求实数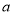 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
 (
( )的圆心为点
)的圆心为点 ,直线
,直线 :
: .
.(1)若
 ,求直线
,求直线 被圆
被圆 所截得弦长的最大值;
所截得弦长的最大值;(2)若直线
 是圆心
是圆心 下方的切线,当
下方的切线,当 在
在 上变化时,求
上变化时,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
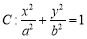
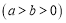 的焦距为2,离心率为
的焦距为2,离心率为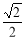 ,
,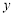 轴上一点
轴上一点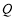 的坐标为
的坐标为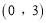 .
.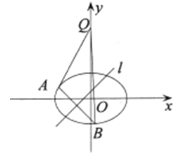
(Ⅰ)求该椭圆的方程;
(Ⅱ)若对于直线
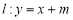 ,椭圆
,椭圆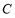 上总存在不同的两点
上总存在不同的两点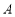 与
与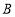 关于直线
关于直线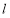 对称,且
对称,且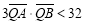 ,求
,求实数
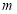 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】
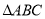 的内角A,B,C的对边分别为a,b,c,已知
的内角A,B,C的对边分别为a,b,c,已知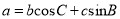
(1)求角B的大小;
(2)若
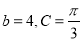 ,求
,求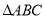 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某企业的两座建筑物AB,CD的高度分别为20m和40m,其底部BD之间距离为20m.为响应创建文明城市号召,进行亮化改造,现欲在建筑物AB的顶部A处安装一投影设备,投影到建筑物CD上形成投影幕墙,既达到亮化目的又可以进行广告宣传.已知投影设备的投影张角∠EAF为
 ,投影幕墙的高度EF越小,投影的图像越清晰.设投影光线的上边沿AE与水平线AG所成角为α,幕墙的高度EF为y(m).
,投影幕墙的高度EF越小,投影的图像越清晰.设投影光线的上边沿AE与水平线AG所成角为α,幕墙的高度EF为y(m).(1)求y关于α的函数关系式
 ,并求出定义域;
,并求出定义域;(2)当投影的图像最清晰时,求幕墙EF的高度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|<
 )在某一个周期内的图象时,列表并填入了部分数据,如下表:
)在某一个周期内的图象时,列表并填入了部分数据,如下表:ωx+φ
0

π

2π
x


Asin(ωx+φ)
0
3
0
-3
0
(1)请将上表数据补充完整,填写在答题卡上相应位置,并直接写出函数f(x)的解析式;
(2)令g(x)=f (x+
 )-
)- ,当x∈[
,当x∈[ ,
,  ]时,恒有不等式g(x)-a-3<0成立,求实数a的取值范围
]时,恒有不等式g(x)-a-3<0成立,求实数a的取值范围
相关试题

