【题目】已知函数![]() (
(![]() ).
).
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)设![]() ,若函数
,若函数![]() 在
在![]() 上为减函数,求实数
上为减函数,求实数![]() 的最小值;
的最小值;
(3)若存在![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)在![]() 递增,在
递增,在![]() 递减.(2)
递减.(2)![]() (3)
(3)![]()
【解析】
试题分析:(1)先求函数导数![]() ,确定导函数零点1,列表分析导函数符号变化规律,确定函数单调区间(2)由题意得
,确定导函数零点1,列表分析导函数符号变化规律,确定函数单调区间(2)由题意得![]()
![]() 在
在![]() 恒成立,即利用变量分离转化为对应函数最值:
恒成立,即利用变量分离转化为对应函数最值:![]() 的最大值,而
的最大值,而![]()
![]() 可视作一个二次函数,根据对称轴与定义区间位置关系得最值(3)不等式存在性问题,一般利用变量分离转化为对应函数最值问题:
可视作一个二次函数,根据对称轴与定义区间位置关系得最值(3)不等式存在性问题,一般利用变量分离转化为对应函数最值问题:![]() ,设
,设![]() ,则
,则![]() ,所以
,所以![]() ,也可分类讨论
,也可分类讨论
试题解析:(1)![]() 时,
时,![]() ,
,![]() ,
,
令![]() ,解得
,解得![]() ,令
,令![]() ,解得
,解得![]() ,
,
∴![]() 在
在![]() 递增,在
递增,在![]() 递减.
递减.
(2)由已知得![]() ,函数的定义域为
,函数的定义域为![]() ,
,
函数![]() 在
在![]() 上为减函数,∴
上为减函数,∴![]()
![]() 在
在![]() 恒成立,
恒成立,
即![]()
![]() 在
在![]() 恒成立.
恒成立.
令![]() ,则
,则![]() ,得到
,得到![]() 在
在![]() 恒成立,得
恒成立,得![]() ,即
,即![]() 的最小值为
的最小值为![]() .
.
(3)若存在![]() ,使得
,使得![]() 成立,
成立,
问题等价于:存在![]() ,使得
,使得![]() 成立,
成立,
问题等价于:“当![]() 时,有
时,有![]() ”,且
”,且![]() ,
,
∵![]() ,结合(2)知:当
,结合(2)知:当![]() 时,
时,![]() .
.
①当![]() 时,
时,![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 在
在![]() 上单调递减,
上单调递减,
则![]() ,得到
,得到![]() 成立.
成立.
②当![]() 时,不满足题意,综上
时,不满足题意,综上![]()
-
科目: 来源: 题型:
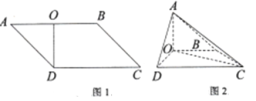
查看答案和解析>>【题目】如图1,在
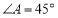 的平行四边形
的平行四边形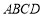 中,
中,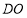 垂直平分
垂直平分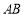 ,且
,且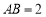 ,现将
,现将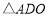 沿
沿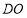 折起(如图2),使
折起(如图2),使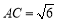 .
.
(Ⅰ)求证:直线
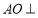 平面
平面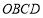 ;
;(Ⅱ)求平面
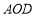 与平面
与平面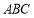 所成的角(锐角)的余弦值.
所成的角(锐角)的余弦值. -
科目: 来源: 题型:
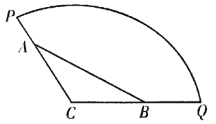
查看答案和解析>>【题目】为方便市民休闲观光,市政府计划在半径为200
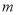 ,圆心角为
,圆心角为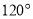 的扇形广场内(如图所示),沿△
的扇形广场内(如图所示),沿△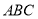 边界修建观光道路,其中
边界修建观光道路,其中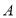 、
、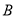 分别在线段
分别在线段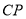 、
、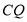 上,且
上,且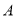 、
、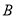 两点间距离为定长
两点间距离为定长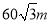 .
.
(1)当
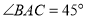 时,求观光道
时,求观光道 段的长度;
段的长度;(2)为提高观光效果,应尽量增加观光道路总长度,试确定图中
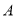 、
、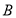 两点的位置,使观光道路总长度达到最长?并求出总长度的最大值.
两点的位置,使观光道路总长度达到最长?并求出总长度的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】判断对错.
(1)若a>b,则ac>bc一定成立.(______)
(2)若a+c>b+d,则a>b,c>d.(______)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
 (
( )的圆心为点
)的圆心为点 ,直线
,直线 :
: .
.(1)若
 ,求直线
,求直线 被圆
被圆 所截得弦长的最大值;
所截得弦长的最大值;(2)若直线
 是圆心
是圆心 下方的切线,当
下方的切线,当 在
在 上变化时,求
上变化时,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
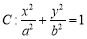
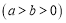 的焦距为2,离心率为
的焦距为2,离心率为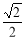 ,
,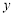 轴上一点
轴上一点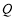 的坐标为
的坐标为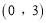 .
.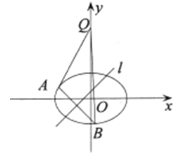
(Ⅰ)求该椭圆的方程;
(Ⅱ)若对于直线
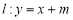 ,椭圆
,椭圆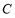 上总存在不同的两点
上总存在不同的两点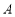 与
与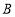 关于直线
关于直线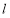 对称,且
对称,且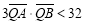 ,求
,求实数
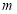 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (
( ).
).(1)若不等式
 的解集为
的解集为 ,求
,求 的取值范围;
的取值范围;(2)当
 时,解不等式
时,解不等式 ;
;(3)若不等式
 的解集为
的解集为 ,若
,若 ,求
,求 的取值范围.
的取值范围.
相关试题

