【题目】已知![]() ,且
,且![]() ,设命题p:函数
,设命题p:函数![]() 在
在![]() 上单调递减;命题q:函数
上单调递减;命题q:函数![]() 在
在![]() 上为增函数,
上为增函数,
(1)若“p且q”为真,求实数c的取值范围
(2)若“p且q”为假,“p或q”为真,求实数c的取值范围.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)∵函数y=cx在R上单调递减,∴0<c<1,即p:0<c<1
又∵f(x)=x2-2cx+1在![]() 上为增函数,∴c≤
上为增函数,∴c≤![]() ,即q:
,即q: ![]() .
.
∴“p且q”为真时,求交集即得解(2)“p或q”为真,“p且q”为假,则p真q假或p假q真.由(1)得p:0<c<1,q: ![]() .∵c>0且c≠1,∴
.∵c>0且c≠1,∴![]() p: c>1,
p: c>1, ![]() q:
q: ![]() 且c≠1.
且c≠1.
分两种情况进行求解最后求并集即可.
试题解析:
(1)∵函数y=cx在R上单调递减,∴0<c<1,即p:0<c<1
又∵f(x)=x2-2cx+1在![]() 上为增函数,∴c≤
上为增函数,∴c≤![]() ,即q:
,即q: ![]() .
.
∴“p且q”为真时, ![]()
(2)∵c>0且c≠1,∴![]() p: c>1,
p: c>1, ![]() q:
q: ![]() 且c≠1.
且c≠1.
又∵“p或q”为真,“p且q”为假,∴p真q假或p假q真.
当p真,q假时,{c|0<c<1}∩{c | ![]() ,且c≠1}={c|
,且c≠1}={c|![]() <c<1}.
<c<1}.
当p假,q真时,{c|c>1}∩{c|0<c≤![]() }=.
}=.
综上所述,实数c的取值范围是{c|![]() <c<1}.
<c<1}.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,a=x,b=2,B=45°,若此三角形有两解,则x的取值范围是( )
A.x>2
B.x<2
C.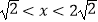
D.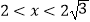
-
科目: 来源: 题型:
查看答案和解析>>【题目】互不相等的三个正数x1 , x2 , x3成等比数列,且点P1(logax1 , logby1)P2(logax2 , logby2),P3(logax3 , logby3)共线(a>0且a≠0,b>且b≠1)则y1 , y2 , y3成( )
A.等差数列,但不等比数列
B.等比数列而非等差数列
C.等比数列,也可能成等差数列
D.既不是等比数列,又不是等差数列 -
科目: 来源: 题型:
查看答案和解析>>【题目】在四棱锥
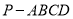 中,
中, 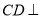 平面
平面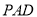 ,
,  ,
, 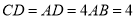 ,且
,且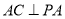 ,
, 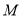 为线段
为线段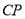 上一点.
上一点.(1)求证:平面
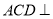 平面
平面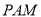 ;
;(2)若
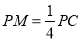 且
且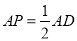 ,求证:
,求证: 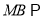 平面
平面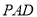 ,并求四棱锥
,并求四棱锥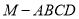 的体积.
的体积.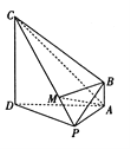
-
科目: 来源: 题型:
查看答案和解析>>【题目】以坐标原点为极点,
 轴的非负半轴为极轴建立极坐标系,已知曲线
轴的非负半轴为极轴建立极坐标系,已知曲线 :
: ,点
,点 的极坐标为
的极坐标为 ,直线
,直线 的极坐标方程为
的极坐标方程为 ,且点
,且点 在直线
在直线 上.
上.(1)求曲线
 的极坐标方程和直线
的极坐标方程和直线 的直角坐标方程;
的直角坐标方程;(2)设
 向左平移
向左平移 个单位长度后得到
个单位长度后得到 ,
, 到
到 的交点为
的交点为 ,
,  ,求
,求 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=2x﹣cosx,{an}是公差为
 的等差数列,f(a1)+f(a2)+…+f(a5)=5π,则[f(a3)]2﹣a1a5=( )
的等差数列,f(a1)+f(a2)+…+f(a5)=5π,则[f(a3)]2﹣a1a5=( )
A.0
B.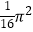
C.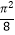
D.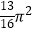
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
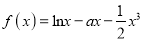 (
(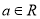 )
)(1)若曲线
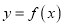 在点
在点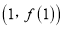 处的切线经过点
处的切线经过点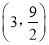 ,求
,求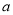 的值;
的值;(2)若
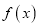 在
在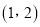 内存在极值,求
内存在极值,求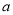 的取值范围;
的取值范围;(3)当
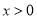 时,
时,  恒成立,求
恒成立,求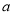 的取值范围.
的取值范围.
相关试题

