【题目】以坐标原点为极点, ![]() 轴的非负半轴为极轴建立极坐标系,已知曲线
轴的非负半轴为极轴建立极坐标系,已知曲线![]() :
:![]() ,点
,点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() ,且点
,且点![]() 在直线
在直线![]() 上.
上.
(1)求曲线![]() 的极坐标方程和直线
的极坐标方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设![]() 向左平移
向左平移![]() 个单位长度后得到
个单位长度后得到![]() ,
,![]() 到
到![]() 的交点为
的交点为![]() ,
, ![]() ,求
,求![]() 的长.
的长.
参考答案:
【答案】(1)![]() ,
, ![]() ;(2)
;(2)![]()
【解析】试题分析:(1)根据![]() 将曲线
将曲线![]() 直角坐标方程化为极坐标方程,将直线
直角坐标方程化为极坐标方程,将直线![]() 的极坐标方程化为直角坐标方程;(2)先根据平移得
的极坐标方程化为直角坐标方程;(2)先根据平移得![]() 的方程,再根据
的方程,再根据![]() 化为极坐标方程,联立方程组可得极径,由极径之差绝对值可得
化为极坐标方程,联立方程组可得极径,由极径之差绝对值可得![]() 的长.
的长.
试题解析:(1)![]() 的直角坐标为
的直角坐标为![]() ,
, ![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
因为![]() 在
在![]() 上,所以
上,所以![]() ,
,
所以![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
![]() :
: ![]() 化为极坐标方程为
化为极坐标方程为![]() .
.
(2)由已知得![]() 的方程为
的方程为![]() ,
,
所以![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() ),
),
代入曲线![]() 的极坐标方程
的极坐标方程![]() 或
或![]() ,所以
,所以![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】互不相等的三个正数x1 , x2 , x3成等比数列,且点P1(logax1 , logby1)P2(logax2 , logby2),P3(logax3 , logby3)共线(a>0且a≠0,b>且b≠1)则y1 , y2 , y3成( )
A.等差数列,但不等比数列
B.等比数列而非等差数列
C.等比数列,也可能成等差数列
D.既不是等比数列,又不是等差数列 -
科目: 来源: 题型:
查看答案和解析>>【题目】在四棱锥
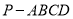 中,
中, 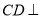 平面
平面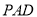 ,
,  ,
, 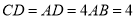 ,且
,且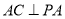 ,
, 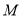 为线段
为线段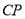 上一点.
上一点.(1)求证:平面
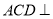 平面
平面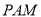 ;
;(2)若
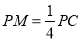 且
且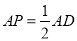 ,求证:
,求证: 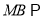 平面
平面 ,并求四棱锥
,并求四棱锥 的体积.
的体积.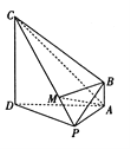
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
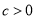 ,且
,且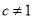 ,设命题p:函数
,设命题p:函数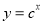 在
在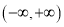 上单调递减;命题q:函数
上单调递减;命题q:函数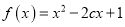 在
在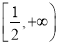 上为增函数,
上为增函数,(1)若“p且q”为真,求实数c的取值范围
(2)若“p且q”为假,“p或q”为真,求实数c的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=2x﹣cosx,{an}是公差为
 的等差数列,f(a1)+f(a2)+…+f(a5)=5π,则[f(a3)]2﹣a1a5=( )
的等差数列,f(a1)+f(a2)+…+f(a5)=5π,则[f(a3)]2﹣a1a5=( )
A.0
B.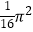
C.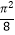
D.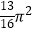
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
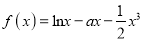 (
(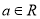 )
)(1)若曲线
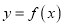 在点
在点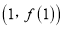 处的切线经过点
处的切线经过点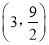 ,求
,求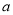 的值;
的值;(2)若
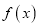 在
在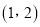 内存在极值,求
内存在极值,求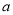 的取值范围;
的取值范围;(3)当
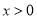 时,
时,  恒成立,求
恒成立,求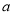 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】宝宝的健康成长是妈妈们最关心的问题,父母亲为婴儿选择什么品牌的奶粉一直以来都是育婴中的一个重要话题,为了解过程奶粉的知名度和消费者的信任度,某调查小组特别调查记录了某大型连锁超市2015年与2016年这两年销售量前5名的五个品牌奶粉的销量(单位:罐),绘制如下的管状图:

(1)根据给出的这两年销量的管状图,对该超市这两年品牌奶粉销量的前五强进行排名;
(2)分别计算这5个品牌奶粉2016年所占总销量(仅指这5个品牌奶粉的总销量)的百分比(百分数精确到各位),并将数据填入如下饼状图中的括号内;

(3)已知该超市2014年飞鹤奶粉的销量为
 (单位:罐),试以
(单位:罐),试以 这3年的销量得出销量
这3年的销量得出销量 关于
关于 年份的线性回归方程,并据此预测2017年该超市飞鹤奶粉的销量.
年份的线性回归方程,并据此预测2017年该超市飞鹤奶粉的销量.相关公式:
 .
.
相关试题

