【题目】一种药在病人血液中的含量不低于2克时,它才能起到有效治疗的作用.已知每服用m(![]() 且
且![]() )个单位的药剂,药剂在血液中的含量y(克)随着时间x(时)变化的函数关系式近似为
)个单位的药剂,药剂在血液中的含量y(克)随着时间x(时)变化的函数关系式近似为![]() ,其中
,其中 .
.
(1)若病人一次服用3个单位的药剂,则有效治疗时间可达多少小时?
(2)若病人第一次服用2个单位的药剂,4个小时后再服用m个单位的药剂,要使接下来的2个小时中能够持续有效治疗,试求m的最小值.
参考答案:
【答案】(1)![]() 小时(2)m的最小值为1
小时(2)m的最小值为1
【解析】
(1)当![]() 时,
时, ,解
,解![]() 时,
时,![]() 的取值范围;
的取值范围;
(2)由条件可知,当![]() 时,血液内药量含量
时,血液内药量含量 ,若药剂有效,需满足
,若药剂有效,需满足![]() 恒成立,参变分离求
恒成立,参变分离求![]() 的取值范围.
的取值范围.
(1)因为![]() ,所以
,所以 .
.
当![]() 时,由
时,由![]() ,解得
,解得![]() ,此时
,此时![]() ;
;
当![]() 时,由
时,由![]() ,解得
,解得![]() ,此时
,此时![]() .
.
综上所述,![]() .
.
所以若一次服用3个单位的药剂,则有效治疗的时间可达![]() 小时.
小时.
(2)当![]() 时,
时, ,
,
因为![]() 对
对![]() 恒成立,
恒成立,
即![]() 对
对![]() 恒成立,等价于
恒成立,等价于
令![]() ,则函数
,则函数![]() 在
在![]() 上是单调递增函数,
上是单调递增函数,
所以当![]() 时,函数
时,函数![]() 取得最大值为1,所以
取得最大值为1,所以![]() ,
,
所以所求m的最小值为1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】中国的钨矿资源储量丰富,在全球已经探明的钨矿产资源储量中占比近
 ,居全球首位。中国又属赣州钨矿资源最为丰富,其素有“世界钨都”之称。某科研单位在研发的钨合金产品的过程中发现了一种新合金材料,由大数据测得该产品的性能指标值与这种新合金材料的含量x(单位:克)的关系为:当
,居全球首位。中国又属赣州钨矿资源最为丰富,其素有“世界钨都”之称。某科研单位在研发的钨合金产品的过程中发现了一种新合金材料,由大数据测得该产品的性能指标值与这种新合金材料的含量x(单位:克)的关系为:当 时,
时,  是
是 的二次函数;当
的二次函数;当 时,
时,  .测得部分数据如表.
.测得部分数据如表.x(单位:克)
0
1
2
9
…
y
0

3

…
(1)求y关于x的函数关系式y=

(2)求函数
 的最大值
的最大值 -
科目: 来源: 题型:
查看答案和解析>>【题目】函数
 的定义域为
的定义域为 ,且对任意
,且对任意 ,有
,有 ,且当
,且当 时
时 .
.(1)证明:
 是奇函数;
是奇函数;(2)证明:
 在
在 上是减函数;
上是减函数;(3)求
 在区间
在区间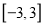 上的最大值和最小值.
上的最大值和最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数

 .若g(x)存在2个零点,则a的取值范围是
.若g(x)存在2个零点,则a的取值范围是A. [–1,0) B. [0,+∞) C. [–1,+∞) D. [1,+∞)
-
科目: 来源: 题型:
查看答案和解析>>【题目】公交车的数量太多容易造成资源浪费,太少又难以满足乘客的需求,为了合理布置车辆,公交公司在2路车的乘客中随机调查了50名乘客,经整理,他们候车时间(单位:
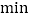 )的茎叶图如下:
)的茎叶图如下:
(Ⅰ)将候车时间分为
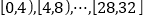 八组,作出相应的频率分布直方图;
八组,作出相应的频率分布直方图;
(Ⅱ)若公交公司将2路车发车时间调整为每隔15
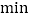 发一趟车,那么上述样本点将发生变化(例如候车时间为9
发一趟车,那么上述样本点将发生变化(例如候车时间为9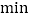 的不变,候车时间为17
的不变,候车时间为17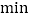 的变为2
的变为2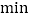 ),现从2路车的乘客中任取5人,设其中候车时间不超过10
),现从2路车的乘客中任取5人,设其中候车时间不超过10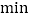 的乘客人数为
的乘客人数为 ,求
,求 的数学期望.
的数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂某种产品的年固定成本为250万元,每生产
 万件,需另投入成本为
万件,需另投入成本为 ,当年产量不足80万件时,
,当年产量不足80万件时, (万元).当年产量不小于80万件时,
(万元).当年产量不小于80万件时, (万元).每件商品售价为50元.通过市场分析,该厂生产的商品能全部售完.
(万元).每件商品售价为50元.通过市场分析,该厂生产的商品能全部售完.(1)写出年利润
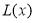 (万元)关于年产量
(万元)关于年产量 (万件)的函数解析式;
(万件)的函数解析式;(2)年产量为多少万件时,该厂在这一商品的生产中所获利润最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
, .
.(1)求函数
 在点
在点 处的切线方程;
处的切线方程;(2)求函数
 的单调区间;
的单调区间;(3) 求证:当
 时,
时, 恒成立.
恒成立.
相关试题

