【题目】椭圆![]() 中心在原点,焦点在
中心在原点,焦点在![]() 轴上,
轴上, ![]() 、
、![]() 分别为上、下焦点,椭圆的离心率为
分别为上、下焦点,椭圆的离心率为![]() ,
, ![]() 为椭圆上一点且
为椭圆上一点且![]() .
.
(1)若![]() 的面积为
的面积为![]() ,求椭圆
,求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() 的延长线与椭圆
的延长线与椭圆![]() 另一交点为
另一交点为![]() ,以
,以![]() 为直径的圆过点
为直径的圆过点 ,
, ![]() 为椭圆上动点,求
为椭圆上动点,求![]() 的范围.
的范围.
参考答案:
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)根据![]() 与椭圆的对称性可得
与椭圆的对称性可得![]() 为椭圆的左、右顶点,再由题设条件列出方程组,即可求出椭圆
为椭圆的左、右顶点,再由题设条件列出方程组,即可求出椭圆![]() 的方程;(2)由离心率得出
的方程;(2)由离心率得出![]() 之间的关系,由
之间的关系,由![]() 为直径的圆过点
为直径的圆过点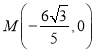 ,可得点
,可得点![]() 横坐标,再根据
横坐标,再根据![]() 三点共线,求出点
三点共线,求出点![]() 纵坐标,将点
纵坐标,将点![]() 坐标代入到椭圆方程化简可求出
坐标代入到椭圆方程化简可求出![]() 的值,即可得到椭圆方程,设点
的值,即可得到椭圆方程,设点![]() ,根据向量坐标表示出
,根据向量坐标表示出![]() ,根据
,根据![]() 取值范围即可求出
取值范围即可求出![]() 的范围.
的范围.
试题解析:(1)由椭圆的对称性可知, ![]() 为椭圆的左、右顶点,可设
为椭圆的左、右顶点,可设![]() ,
,
∴ 解得
解得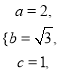 ∴
∴![]() .
.
(2)椭圆的离心率为![]() ,
, ![]() ,则
,则![]() ,
, ![]() ,
, ![]() ,
,
∵以![]() 为直径的圆过点
为直径的圆过点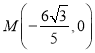 ,∴
,∴![]() .
.
又∵![]() 的延长线与椭圆
的延长线与椭圆![]() 另一交点为
另一交点为![]() ,则
,则![]() 、
、![]() 、
、![]() 三点共线,
三点共线,
∴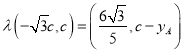 ,∴
,∴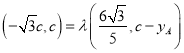 ,
,
∴![]() ,
, ![]() ,
,
又∵![]() 在椭圆中,则代入椭圆方程有
在椭圆中,则代入椭圆方程有![]() ,
, ![]() ,
, ![]() ,
,
设椭圆上动点![]() ,则
,则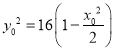 ,
, ![]() ,
,
∴![]()
![]() ,
, ![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数列{an}满足Sn=2n﹣an(n∈N*).
(1)计算a1 , a2 , a3 , a4 , 并由此猜想通项公式an;
(2)用数学归纳法证明(Ⅰ)中的猜想. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知四棱锥P﹣ABCD,底面ABCD是直角梯形,AD∥BC,∠BCD=90°,PA⊥底面ABCD,△ABM是边长为2的等边三角形,
 .
. 
(1)求证:平面PAM⊥平面PDM;
(2)若点E为PC中点,求二面角P﹣MD﹣E的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
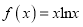 .
.(1)求曲线
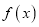 在点
在点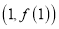 处的切线方程;
处的切线方程;(2)求函数
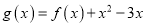 的单调区间及极值;
的单调区间及极值;(3)对
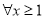 ,
, 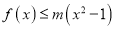 成立,求实数
成立,求实数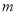 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
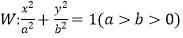 的离心率为
的离心率为 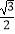 ,其左顶点A在圆O:x2+y2=16上.
,其左顶点A在圆O:x2+y2=16上. 
(1)求椭圆W的方程;
(2)若点P为椭圆W上不同于点A的点,直线AP与圆O的另一个交点为Q.是否存在点P,使得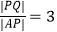 ?若存在,求出点P的坐标;若不存在,说明理由.
?若存在,求出点P的坐标;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,平面
中,平面 平面
平面 ,
, ,
, 是等边三角形,已知
是等边三角形,已知 ,
, .
.
(1)设
 是
是 上的一点,证明:平面
上的一点,证明:平面 平面
平面 ;
;(2)求四棱锥
 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】正方形ABCD一条边AB所在方程为x+3y﹣5=0,另一边CD所在直线方程为x+3y+7=0,
(Ⅰ)求正方形中心G所在的直线方程;
(Ⅱ)设正方形中心G(x0 , y0),当正方形仅有两个顶点在第一象限时,求x0的取值范围.
相关试题

