【题目】如图,在四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() 是等边三角形,已知
是等边三角形,已知![]() ,
,![]() .
.

(1)设![]() 是
是![]() 上的一点,证明:平面
上的一点,证明:平面![]() 平面
平面![]() ;
;
(2)求四棱锥![]() 的体积.
的体积.
参考答案:
【答案】(1)见解析(2)![]()
【解析】试题分析:
(1)证得AD⊥BD,而面PAD⊥面ABCD,∴BD⊥面PAD,∴面MBD⊥面PAD.
(2)作辅助线PO⊥AD,则PO为四棱锥P—ABCD的高,求得S四边形ABCD=24.∴VP—ABCD=16![]() .
.
试题解析:
(1)证明:在△ABD中,∵AD=4,BD=8,AB=4![]() ,∴AD2+BD2=AB2.∴AD⊥BD.
,∴AD2+BD2=AB2.∴AD⊥BD.
又∵面PAD⊥面ABCD,面PAD∩面ABCD=AD,BD面ABCD,∴BD⊥面PAD.
又BD面BDM,∴面MBD⊥面PAD.
(2)解:过P作PO⊥AD,
∵面PAD⊥面ABCD,∴PO⊥面ABCD,即PO为四棱锥P—ABCD的高.
又△PAD是边长为4的等边三角形,∴PO=2![]() .
.
在底面四边形ABCD中,AB∥DC,AB=2DC,∴四边形ABCD为梯形.
在Rt△ADB中,斜边AB边上的高为![]() =
=![]() ,此即为梯形的高.
,此即为梯形的高.
∴S四边形ABCD=![]() ×
×![]() =24.
=24.
∴VP—ABCD=![]() ×24×2
×24×2![]() =16
=16![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
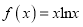 .
.(1)求曲线
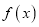 在点
在点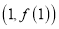 处的切线方程;
处的切线方程;(2)求函数
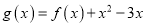 的单调区间及极值;
的单调区间及极值;(3)对
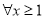 ,
, 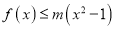 成立,求实数
成立,求实数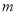 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】椭圆
 中心在原点,焦点在
中心在原点,焦点在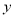 轴上,
轴上,  、
、 分别为上、下焦点,椭圆的离心率为
分别为上、下焦点,椭圆的离心率为 ,
,  为椭圆上一点且
为椭圆上一点且 .
.(1)若
 的面积为
的面积为 ,求椭圆
,求椭圆 的标准方程;
的标准方程;(2)若
 的延长线与椭圆
的延长线与椭圆 另一交点为
另一交点为 ,以
,以 为直径的圆过点
为直径的圆过点 ,
,  为椭圆上动点,求
为椭圆上动点,求 的范围.
的范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
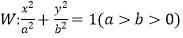 的离心率为
的离心率为 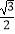 ,其左顶点A在圆O:x2+y2=16上.
,其左顶点A在圆O:x2+y2=16上. 
(1)求椭圆W的方程;
(2)若点P为椭圆W上不同于点A的点,直线AP与圆O的另一个交点为Q.是否存在点P,使得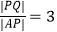 ?若存在,求出点P的坐标;若不存在,说明理由.
?若存在,求出点P的坐标;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】正方形ABCD一条边AB所在方程为x+3y﹣5=0,另一边CD所在直线方程为x+3y+7=0,
(Ⅰ)求正方形中心G所在的直线方程;
(Ⅱ)设正方形中心G(x0 , y0),当正方形仅有两个顶点在第一象限时,求x0的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 (x>0).
(x>0).
(1)试判断函数f(x)在(0,+∞)上单调性并证明你的结论;
(2)若f(x)> 恒成立,求整数k的最大值;
恒成立,求整数k的最大值;
(3)求证:(1+1×2)(1+2×3)…[1+n(n+1)]>e2n﹣3 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知O是△ABC内一点,若
 , 则△AOC与△ABC的面积的比值为 ( )
, 则△AOC与△ABC的面积的比值为 ( )
A.
B.
C.
D.
相关试题

