【题目】质检部门对某工厂甲、乙两个车间生产的12个零件质量进行检测.甲、乙两个车间的零件质量(单位:克)分布的茎叶图如图所示.零件质量不超过20克的为合格.
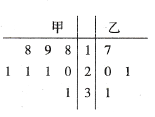
(1)从甲、乙两车间分别随机抽取2个零件,求甲车间至少一个零件合格且乙车间至少一个零件合格的概率;
(2)质检部门从甲车间8个零件中随机抽取4件进行检测,若至少2件合格,检测即可通过,若至少3 件合格,检测即为良好,求甲车间在这次检测通过的条件下,获得检测良好的概率;
(3)若从甲、乙两车间12个零件中随机抽取2个零件,用![]() 表示乙车间的零件个数,求
表示乙车间的零件个数,求![]() 的分布列与数学期望.
的分布列与数学期望.
参考答案:
【答案】(1)![]() (2)
(2)![]() (3)分布列见解析
(3)分布列见解析![]()
【解析】试题分析:
(1)本题求独立事件同时发生的概率,解题时运用对立事件的概率求解比较简单.(2)运用条件概率求解,解题时要分清谁是条件.(3)由题意可得到![]() 的所有可能取值,然后分别求出概率,列成表格的形式可得分布列,根据定义求得期望值.
的所有可能取值,然后分别求出概率,列成表格的形式可得分布列,根据定义求得期望值.
试题解析:
(1)由题意得甲车间的合格零件数为4,乙车间的合格的零件数为2,
故所求概率为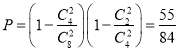 .
.
即甲车间至少一个零件合格且乙车间至少一个零件合格的概率为![]() .
.
(2)设事件![]() 表示“2件合格,2件不合格”;事件
表示“2件合格,2件不合格”;事件![]() 表示“3件合格,1件不合格”;事件
表示“3件合格,1件不合格”;事件![]() 表示“4件全合格”; 事件
表示“4件全合格”; 事件![]() 表示“检测通过”;事件
表示“检测通过”;事件![]() 表示“检测良好”.
表示“检测良好”.
则![]() ,
,
∴![]() .
.
故甲车间在这次检测通过的条件下,获得检测良好的概率为![]() .
.
(3)由题意可得![]() 的所有可能取值为0,1,2.
的所有可能取值为0,1,2.
![]() ,
,
![]() ,
,
![]() .
.
∴ 随机变量![]() 的分布列为
的分布列为
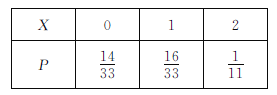
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学调查了某班全部
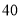 名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)
名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)
(1)能否由
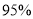 的把握认为参加书法社团和参加演讲社团有关?
的把握认为参加书法社团和参加演讲社团有关?(附:
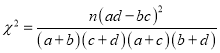
当
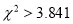 时,有
时,有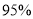 的把握说事件
的把握说事件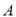 与
与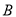 有关;当
有关;当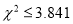 ,认为事件
,认为事件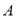 与
与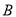 是无关的)
是无关的)(2)已知既参加书法社团又参加演讲社团的
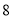 名同学中,有
名同学中,有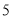 名男同学,
名男同学, 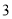 名女同学.现从这
名女同学.现从这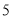 名男同学和
名男同学和 名女同学中选
名女同学中选 人参加综合素质大赛,求被选中的男生人数
人参加综合素质大赛,求被选中的男生人数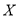 的分布列和期望.
的分布列和期望. -
科目: 来源: 题型:
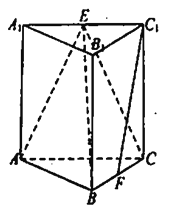
查看答案和解析>>【题目】如图,在直三棱柱
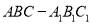 中,
中, 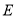 、
、 分别为
分别为 、
、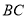 的中点,
的中点, 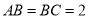 ,
,  .
.
(1)求证:平面
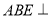 平面
平面 ;
;(2)若直线
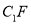 和平面
和平面 所成角的正弦值等于
所成角的正弦值等于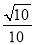 ,求二面角
,求二面角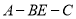 的平面角的正弦值.
的平面角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
 中,以坐标原点
中,以坐标原点 为极点,以
为极点,以 轴正半轴为极轴,建立极坐标系.曲线
轴正半轴为极轴,建立极坐标系.曲线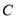 的极坐标方程为
的极坐标方程为 ,曲线
,曲线 的参数方程为
的参数方程为 (
( 为参数)
为参数)(1)求曲线
 的直角坐标方程及曲线
的直角坐标方程及曲线 的极坐标方程;
的极坐标方程;(2)当
 (
( )时在曲线
)时在曲线 上对应的点为
上对应的点为 ,若
,若 的面积为
的面积为 ,求
,求 点的极坐标,并判断
点的极坐标,并判断 是否在曲线
是否在曲线 上(其中点
上(其中点 为半圆的圆心)
为半圆的圆心) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在底面为正方形的四棱柱
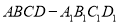 中,
中, 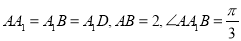 .
.
(1)证明:平面
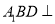 平面
平面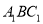 ;
;(2)求直线
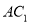 与平面
与平面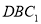 所成角的正弦值.
所成角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
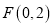 ,过点
,过点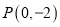 且与
且与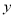 轴垂直的直线为
轴垂直的直线为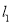 ,
, 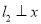 轴,交
轴,交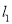 于点
于点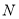 ,直线
,直线 垂直平分
垂直平分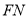 ,交
,交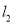 于点
于点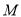 .
.(1)求点
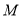 的轨迹方程;
的轨迹方程;(2)记点
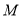 的轨迹为曲线
的轨迹为曲线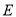 ,直线
,直线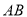 与曲线
与曲线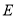 交于不同两点
交于不同两点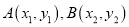 ,且
,且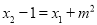 (
(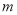 为常数),直线
为常数),直线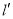 与
与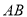 平行,且与曲线
平行,且与曲线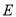 相切,切点为
相切,切点为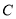 ,试问
,试问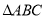 的面积是否为定值.若为定值,求出
的面积是否为定值.若为定值,求出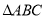 的面积;若不是定值,说明理由.
的面积;若不是定值,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】【2018百校联盟TOP20一月联考】函数
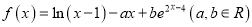 在
在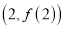 处的切线斜率为
处的切线斜率为 .
.(I)讨论函数
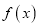 的单调性;
的单调性; (II)设
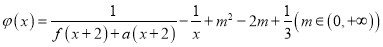 ,
, 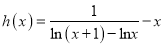 ,对任意的
,对任意的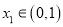 ,存在
,存在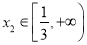 ,使得
,使得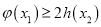 成立,求
成立,求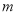 的取值范围.
的取值范围.
相关试题

