【题目】某中学调查了某班全部![]() 名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)
名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)

(1)能否由![]() 的把握认为参加书法社团和参加演讲社团有关?
的把握认为参加书法社团和参加演讲社团有关?
(附: 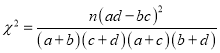
当![]() 时,有
时,有![]() 的把握说事件
的把握说事件![]() 与
与![]() 有关;当
有关;当![]() ,认为事件
,认为事件![]() 与
与![]() 是无关的)
是无关的)
(2)已知既参加书法社团又参加演讲社团的![]() 名同学中,有
名同学中,有![]() 名男同学,
名男同学, ![]() 名女同学.现从这
名女同学.现从这![]() 名男同学和
名男同学和![]() 名女同学中选
名女同学中选![]() 人参加综合素质大赛,求被选中的男生人数
人参加综合素质大赛,求被选中的男生人数![]() 的分布列和期望.
的分布列和期望.
参考答案:
【答案】(1)见解析;(2)见解析.
【解析】试题分析:(1)根据表格中的数据得到![]() ,此时可以下结论;(2)根据题意分别求出
,此时可以下结论;(2)根据题意分别求出![]() 的取值为
的取值为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,时的概率值,再写出分布列和期望值即可。
,时的概率值,再写出分布列和期望值即可。
解析:
(1)由调查数据可知, ![]()
没有![]() 的把握认为参加书法社团和参加演讲社团有关.
的把握认为参加书法社团和参加演讲社团有关.
(2)被选中的男生人数![]() 的取值为
的取值为![]() ,
, ![]() ,
, ![]() ,
, ![]()
则![]()
![]()
![]()
![]()
分布列为
|
|
|
|
|
|
|
|
|
|
期望![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直三棱柱
 中,
中,  、
、 分别为
分别为 、
、 的中点,
的中点,  ,
,  .
.
(1)求证:
 平面
平面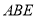 ;
;(2)求三棱锥
 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
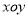 中,以坐标原点
中,以坐标原点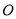 为极点,以
为极点,以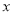 轴正半轴为极轴,建立极坐标系.曲线
轴正半轴为极轴,建立极坐标系.曲线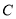 的极坐标方程为
的极坐标方程为 ,曲线
,曲线 的参数方程为
的参数方程为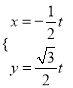 (
( 为参数)
为参数)(1)求曲线
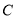 的直角坐标方程及曲线
的直角坐标方程及曲线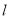 的极坐标方程;
的极坐标方程;(2)当
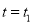 (
(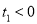 )时在曲线
)时在曲线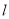 上对应的点为
上对应的点为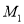 ,若
,若 的面积为
的面积为 ,求
,求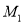 点的极坐标,并判断
点的极坐标,并判断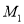 是否在曲线
是否在曲线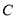 上(其中点
上(其中点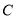 为半圆的圆心)
为半圆的圆心) -
科目: 来源: 题型:
查看答案和解析>>【题目】某校初三年级有
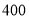 名学生,随机抽查了
名学生,随机抽查了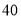 名学生,测试
名学生,测试 分钟仰卧起坐的成绩(次数),将数据整理后绘制成如图所示的频率分布直方图.用样本估计总体,下列结论正确的是( )
分钟仰卧起坐的成绩(次数),将数据整理后绘制成如图所示的频率分布直方图.用样本估计总体,下列结论正确的是( )
A. 该校初三年级学生
 分钟仰卧起坐的次数的中位数为
分钟仰卧起坐的次数的中位数为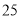 次
次B. 该校初三年级学生
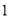 分钟仰卧起坐的次数的众数为
分钟仰卧起坐的次数的众数为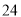 次
次C. 该校初三年级学生
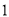 分钟仰卧起坐的次数超过
分钟仰卧起坐的次数超过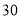 次的人数约有
次的人数约有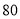 人
人D. 该校初三年级学生
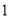 分钟仰卧起坐的次数少于
分钟仰卧起坐的次数少于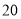 次的人数约为
次的人数约为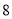 人.
人. -
科目: 来源: 题型:
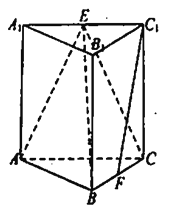
查看答案和解析>>【题目】如图,在直三棱柱
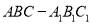 中,
中, 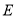 、
、 分别为
分别为 、
、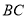 的中点,
的中点, 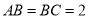 ,
,  .
.
(1)求证:平面
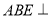 平面
平面 ;
;(2)若直线
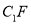 和平面
和平面 所成角的正弦值等于
所成角的正弦值等于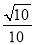 ,求二面角
,求二面角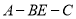 的平面角的正弦值.
的平面角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
 中,以坐标原点
中,以坐标原点 为极点,以
为极点,以 轴正半轴为极轴,建立极坐标系.曲线
轴正半轴为极轴,建立极坐标系.曲线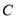 的极坐标方程为
的极坐标方程为 ,曲线
,曲线 的参数方程为
的参数方程为 (
( 为参数)
为参数)(1)求曲线
 的直角坐标方程及曲线
的直角坐标方程及曲线 的极坐标方程;
的极坐标方程;(2)当
 (
( )时在曲线
)时在曲线 上对应的点为
上对应的点为 ,若
,若 的面积为
的面积为 ,求
,求 点的极坐标,并判断
点的极坐标,并判断 是否在曲线
是否在曲线 上(其中点
上(其中点 为半圆的圆心)
为半圆的圆心) -
科目: 来源: 题型:
查看答案和解析>>【题目】质检部门对某工厂甲、乙两个车间生产的12个零件质量进行检测.甲、乙两个车间的零件质量(单位:克)分布的茎叶图如图所示.零件质量不超过20克的为合格.
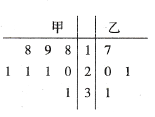
(1)从甲、乙两车间分别随机抽取2个零件,求甲车间至少一个零件合格且乙车间至少一个零件合格的概率;
(2)质检部门从甲车间8个零件中随机抽取4件进行检测,若至少2件合格,检测即可通过,若至少3 件合格,检测即为良好,求甲车间在这次检测通过的条件下,获得检测良好的概率;
(3)若从甲、乙两车间12个零件中随机抽取2个零件,用
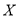 表示乙车间的零件个数,求
表示乙车间的零件个数,求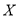 的分布列与数学期望.
的分布列与数学期望.
相关试题

