【题目】已知函数![]() 的最小值为0,其中
的最小值为0,其中![]() ,设
,设![]() .
.
(1)求![]() 的值;
的值;
(2)对任意![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)讨论方程![]() 在
在![]() 上根的个数.
上根的个数.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)由图像知
;(3)由图像知![]() 时有一个根,
时有一个根,![]() 时无根.
时无根.
【解析】
试题分析:(1)首先求出函数的定义域,并求出其导函数,然后令![]() 求出极值点,并判断导函数的符号进而得出函数取得极值,进而得出其最小值,即可得出结果;(2)首先将问题转化为
求出极值点,并判断导函数的符号进而得出函数取得极值,进而得出其最小值,即可得出结果;(2)首先将问题转化为![]() 对
对![]() 恒成立,于是构造函数
恒成立,于是构造函数![]() ,再利用导数判断其单调性,最后得出实数
,再利用导数判断其单调性,最后得出实数![]() 的取值范围;(3)首先将问题转化为
的取值范围;(3)首先将问题转化为![]() ,然后转化为
,然后转化为![]() ,最后利用导数和函数的图像即可得出所求的结果
,最后利用导数和函数的图像即可得出所求的结果
试题解析:(1)![]() 的定义域为
的定义域为![]() .
.![]()
由![]() ,解得x=1-a>-a.
,解得x=1-a>-a.
当x变化时,![]() ,
,![]() 的变化情况如下表:
的变化情况如下表:
x | (-a,1-a) | 1-a | (1-a,+∞) |
| - | 0 | + |
|
| 极小值 |
|
因此,![]() 在
在![]() 处取得最小值,故由题意
处取得最小值,故由题意![]() ,所以
,所以![]() .
.
(2)由![]() 知
知![]() 对
对![]() 恒成立
恒成立
即![]() 是
是![]() 上的减函数.
上的减函数.
![]() 对
对![]() 恒成立,
恒成立,![]() 对
对![]() 恒成立
恒成立
![]() ,
,![]()
(3)由题意知![]() ,
,![]()
由图像知![]() 时有一个根,
时有一个根,![]() 时无根
时无根
或解:![]() ,
,![]() ,又可求得
,又可求得![]() 时
时![]() .
.![]() 在
在![]() 时 单调递增.
时 单调递增.![]() 时,
时,![]() ,
,![]() 时有一个根,
时有一个根,![]() 时无根.
时无根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一直径为8米的半圆形空地,现计划种植甲、乙两种水果,已知单位面积种植甲水果的经济价值是种植乙水果经济价值的5倍,但种植甲水果需要有辅助光照.半圆周上的
 处恰有一可旋转光源满足甲水果生长的需要,该光源照射范围是
处恰有一可旋转光源满足甲水果生长的需要,该光源照射范围是 ,点
,点 在直径
在直径 上,且
上,且 .
.
(1)若
 米,求
米,求 的长;
的长;(2)设
 , 求该空地产生最大经济价值时种植甲种水果的面积.
, 求该空地产生最大经济价值时种植甲种水果的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
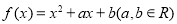 的一个零点为-2,当
的一个零点为-2,当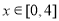 时最大值为0.
时最大值为0.(1)求
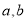 的值;
的值;(2)若对
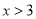 ,不等式
,不等式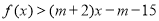 恒成立,求实数
恒成立,求实数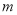 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等比数列{an}的公比q>1,且满足a2+a3+a4=28,且a3+2是a2,a4的等差中项.
(1)求数列{an}的通项公式;
(2)若bn=log
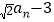 ,Sn=b1+b2+…+bn,求使
,Sn=b1+b2+…+bn,求使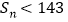 成立的正整数n的最大值.
成立的正整数n的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知两条直线l1:ax﹣by+4=0,l2:(a﹣1)x+y+b=0. 求满足下列条件的a,b值.
(Ⅰ)l1⊥l2且l1过点(﹣3,﹣1);
(Ⅱ)l1∥l2且原点到这两直线的距离相等.
-
科目: 来源: 题型:
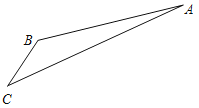
查看答案和解析>>【题目】如图,游客从某旅游景区的景点A处下山至C处有两种路径.一种是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客从A处下山,甲沿AC匀速步行,速度为50m/min.在甲出发2min后,乙从A乘缆车到B,在B处停留1min后,再从B匀速步行到C.假设缆车匀速直线运动的速度为130m/min,山路AC长为1260m,经测量,
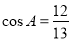 ,
,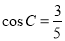 .
.
(Ⅰ)问乙出发多少分钟后,乙在缆车上与甲的距离最短?
(Ⅱ)为使两位游客在
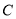 处互相等待的时间不超过
处互相等待的时间不超过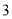 分钟,乙步行的速度应控制在什么范围内?
分钟,乙步行的速度应控制在什么范围内? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知在锐角△ABC中,两向量p=(2-2sin A,cos A+sin A),q=(sin A-cos A,1+sin A),且p与q是共线向量.
(1)求A的大小;
(2)求函数y=2sin2B+cos(
 )取最大值时,角B的大小.
)取最大值时,角B的大小.
相关试题

