【题目】小丽今天晚自习准备复习历史、地理或政治中的一科,她用数学游戏的结果来决定选哪一科,游戏规则是:在平面直角坐标系中,以原点![]() 为起点,再分别以
为起点,再分别以![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 这5个点为终点,得到5个向量,任取其中两个向量,计算这两个向量的数量积
这5个点为终点,得到5个向量,任取其中两个向量,计算这两个向量的数量积![]() ,若
,若![]() ,就复习历史,若
,就复习历史,若![]() ,就复习地理,若
,就复习地理,若![]() ,就复习政治.
,就复习政治.
(1)写出![]() 的所有可能取值;
的所有可能取值;
(2)求小丽复习历史的概率和复习地理的概率.
参考答案:
【答案】(Ⅰ)y的所有可能取值为![]() ;(Ⅱ)
;(Ⅱ) ![]() .
.
【解析】试题分析:(Ⅰ)依次求出所有向量的数量积;(Ⅱ)任取两个向量的所有可能情况总数有10种,计算![]() 的情况和
的情况和![]() 的情况有的个数即可.
的情况有的个数即可.
试题解析:
(Ⅰ)依题意计算
![]() ,
,
![]() ,
,
![]() ,
,
所以y的所有可能取值为![]() .
.
(Ⅱ)任取两个向量的所有可能情况总数有10种,
其中![]() 的情况有4种,所以小丽复习历史的概率为
的情况有4种,所以小丽复习历史的概率为![]() ,
,
![]() 的情况有3种,所以小丽复习地理的概率为
的情况有3种,所以小丽复习地理的概率为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了让学生更多的了解“数学史”知识,梁才学校高二年级举办了一次“追寻先哲的足迹,倾听数学的声音”的数学史知识竞赛活动,共有800名学生参加了这次竞赛.为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计,统计结果见下表.请你根据频率分布表解答下列问题:
序号
分组
组中值
频数
频率
(i)
(分数)
(Gi)
(人数)
(Fi)
1

65
①
0.12
2

75
20
②
3

85
③
0.24
4

95
④
⑤
合计
50
1
(1)填充频率分布表中的空格;
(2)为鼓励更多的学生了解“数学史”知识,成绩不低于85分的同学能获奖,请估计在
参加的800名学生中大概有多少名学生获奖?(3)在上述统计数据的分析中有一项计算见算法流程图,求输出的S的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=﹣
 +bx+c与y轴交于点C,与x轴的两个交点分别为A(﹣4,0),B(1,0).
+bx+c与y轴交于点C,与x轴的两个交点分别为A(﹣4,0),B(1,0).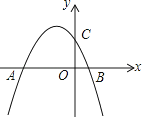
(1)求抛物线的解析式;
(2)已知点P在抛物线上,连接PC,PB,若△PBC是以BC为直角边的直角三角形,求点P的坐标;
(3)已知点E在x轴上,点F在抛物线上,是否存在以A,C,E,F为顶点的四边形是平行四边形?若存在,请直接写出点E的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了节约水资源,某市准备按照居民家庭年用水量实行阶梯水价.水价分档递增,计划使第一档、第二档和第三档的水价分别覆盖全市居民家庭的80%,15%和5%,为合理确定各档之间的界限,随机抽查了该市5万户居民家庭上一年的年用水量(单位:m3),绘制了统计图.如图所示,下面四个推断( )
①年用水量不超过180m3的该市居民家庭按第一档水价交费;
②年用水量超过240m3的该市居民家庭按第三档水价交费;
③该市居民家庭年用水量的中位数在150﹣180之间;
④该市居民家庭年用水量的平均数不超过180.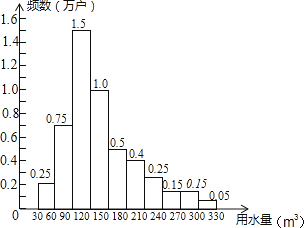
A.①③
B.①④
C.②③
D.②④ -
科目: 来源: 题型:
查看答案和解析>>【题目】“五一”假期期间,某餐厅对选择
 、
、 、
、 三种套餐的顾客进行优惠。对选择
三种套餐的顾客进行优惠。对选择 、
、 套餐的顾客都优惠10元,对选择
套餐的顾客都优惠10元,对选择 套餐的顾客优惠20元。根据以往“五一”假期期间100名顾客对选择
套餐的顾客优惠20元。根据以往“五一”假期期间100名顾客对选择 、
、 、
、 三种套餐的情况得到下表:
三种套餐的情况得到下表:选择套餐种类



选择每种套餐的人数
50
25
25
将频率视为概率.
(I)若有甲、乙、丙三位顾客选择某种套餐,求三位顾客选择的套餐至少有两样不同的概率;
(II)若用随机变量
 表示两位顾客所得优惠金额的综合,求
表示两位顾客所得优惠金额的综合,求 的分布列和期望。
的分布列和期望。 -
科目: 来源: 题型:
查看答案和解析>>【题目】林业部门要考察某种幼树在一定条件下的移植成活率,下表是这种幼树在移植过程中的一组数据:
移植的棵数n
1000
1500
2500
4000
8000
15000
20000
30000
成活的棵数m
865
1356
2220
3500
7056
13170
17580
26430
成活的频率

0.865
0.904
0.888
0.875
0.882
0.878
0.879
0.881
估计该种幼树在此条件下移植成活的概率为 .
-
科目: 来源: 题型:
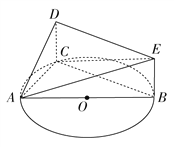
查看答案和解析>>【题目】如图,AB是圆O的直径,点C在圆O上,矩形DCBE所在的平面垂直于圆O所在的平面,
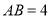 ,
, 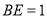 .
.(1)若
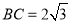 ,求三棱锥
,求三棱锥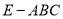 的体积;
的体积;(2)证明:平面ACD⊥平面BCDE;
相关试题

