【题目】【四川省高2017届第一次名校联考(广志联考)(理)】已知函数![]() .
.
(Ⅰ)当![]() 时,存在
时,存在![]() 使不等式
使不等式![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)若在区间![]() 上,函数
上,函数![]() 的图象恒在直线
的图象恒在直线![]() 的下方,求实数
的下方,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(I)![]() ;(II)详见解析.
;(II)详见解析.
【解析】试题分析:
试题解析:(I)借助存在型不等式成立的条件建立不等式;(II)先建立不等式,再运用导数知识求解:
解:(Ⅰ)当![]() 时,
时,![]() ,
,
所以![]() ,由
,由![]() 知
知![]() ,
,
则函数![]() 在区间
在区间![]() 为增函数,
为增函数,
则当![]() 时,
时,![]() ,
,
故存在![]() 使不等式
使不等式![]() 成立,
成立,
只需![]() 即可.
即可.
(Ⅱ)在区间![]() 上,函数
上,函数![]() 的图象恒在直线
的图象恒在直线![]() 的下方等价于对任意
的下方等价于对任意![]() ,
,![]() ,
,
即![]() 恒成立,
恒成立,
设![]() ,
,![]() .
.
则![]()
当![]() 时,
时,![]() ,
,![]() .
.
①若![]() ,即
,即![]() ,有
,有![]() ,
,
则函数![]() 在区间
在区间![]() 为减函数,
为减函数,
则对任意![]() ,
,![]() ,
,
只需![]() ,即当
,即当![]() 时,
时,![]() 恒成立.
恒成立.
②若![]() ,即
,即![]() 时,
时,
令![]() ,
,
得![]() .
.
则函数![]() 在区间
在区间![]() 为减函数,在区间
为减函数,在区间![]() 为增函数,
为增函数,
则![]() ,不合题意.
,不合题意.
③若![]() ,即当
,即当![]() 时,
时,![]() ,函数
,函数![]() 在区间
在区间![]() 为增函数,
为增函数,
则![]() ,不合题意.
,不合题意.
综上,当![]() 时,
时,![]() 在区间
在区间![]() 恒成立,
恒成立,
即当![]() 时,在区间
时,在区间![]() 上函数
上函数![]() 的图象恒在直线
的图象恒在直线![]() 的下方.
的下方.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,其中
,其中 为常数.
为常数. (1)判断函数
 的单调性并证明;
的单调性并证明;(2)当
 时,对于任意
时,对于任意 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正四棱锥P-ABCD中,底面边长为2,侧棱长为
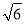 ,M,N分别为AB,BC的中点,以O为原点,射线OM,ON,OP分别为x轴、y轴、z轴的正方向建立空间直角坐标系.若E,F分别为PA,PB的中点,求A,B,C,D,E,F的坐标.
,M,N分别为AB,BC的中点,以O为原点,射线OM,ON,OP分别为x轴、y轴、z轴的正方向建立空间直角坐标系.若E,F分别为PA,PB的中点,求A,B,C,D,E,F的坐标.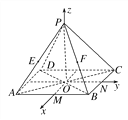
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
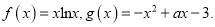
(1)求函数
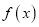 在区间
在区间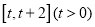 上的最小值;
上的最小值;(2)对一切实数
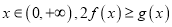 恒成立,求实数
恒成立,求实数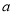 的取值范围;
的取值范围;(3)证明:对一切
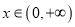 ,
, 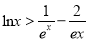 恒成立.
恒成立. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知三点A(-1,1,2),B(1,2,-1),C(a,0,3),是否存在实数a,使A、B、C共线?若存在,求出a的值;若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数
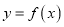 的导函数的图象如图所示,给出下列判断:
的导函数的图象如图所示,给出下列判断:①函数
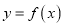 在区间
在区间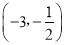 内单调递增;②函数
内单调递增;②函数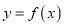 在区间
在区间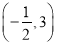 内单调递减;③函数
内单调递减;③函数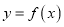 在区间
在区间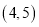 内单调递增;④当
内单调递增;④当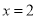 时,函数
时,函数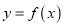 有极小值;⑤当
有极小值;⑤当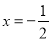 时,函数
时,函数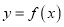 有极大值.则上述判断中正确的是( )
有极大值.则上述判断中正确的是( )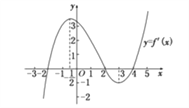
A. ①② B. ③
C. ②③ D. ③④⑤
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 是半圆
是半圆 的直径,
的直径, ,
, 是将半圆圆周四等分的三个分点.
是将半圆圆周四等分的三个分点.
(1)从
 这5个点中任取3个点,求这3个点组成直角三角形的概率;
这5个点中任取3个点,求这3个点组成直角三角形的概率;(2)在半圆内任取一点
 ,求
,求 的面积大于
的面积大于 的概率.
的概率.
相关试题

