【题目】已知![]()
(1)求函数![]() 在区间
在区间![]() 上的最小值;
上的最小值;
(2)对一切实数![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)证明:对一切![]() ,
, ![]() 恒成立.
恒成立.
参考答案:
【答案】(1)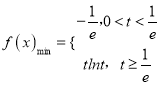 ;(2)4;(3)见解析.
;(2)4;(3)见解析.
【解析】试题分析:(1)求出![]() ,分三种情况讨论,分别令
,分三种情况讨论,分别令 ![]() 得增区间,
得增区间, ![]() 得减区间,从而可得函数
得减区间,从而可得函数![]() 在区间
在区间![]() 上的最小值;(2)
上的最小值;(2)![]() 等价于
等价于![]() ,只需以
,只需以![]() 即可;(3)问题等价于证明
即可;(3)问题等价于证明![]() ,由
,由![]() 的最小值是
的最小值是![]() ,
, ![]() 最大值为
最大值为![]() .
.
试题解析:(1)![]() ,当
,当![]() ,
, ![]() ,
, ![]() 单调递减,当
单调递减,当![]() ,
, ![]() ,
,
![]() 单调递增.············ 2分
单调递增.············ 2分
①![]() ,t无解;
,t无解;
②![]() ,即
,即![]() 时,
时, ![]()
③![]() ,即
,即![]() 时,
时, ![]() 在
在![]() 上单调递增,
上单调递增, ![]()
所以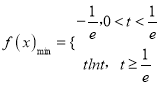 .········· 5分
.········· 5分
(2)![]() ,则
,则![]() ,
,
设![]() ,则
,则![]() ,
,
![]() ,
, ![]() ,
, ![]() 单调递增,
单调递增, ![]() ,
, ![]() ,
,
![]() 单调递减,所以
单调递减,所以![]() ,因为对一切
,因为对一切![]() ,
, ![]() 恒成立,
恒成立,
所以![]() ;
;
(3)问题等价于证明![]() ,
,
由⑴可知![]() 的最小值是
的最小值是![]() ,当且仅当
,当且仅当![]() 时取到,
时取到,
设![]() ,则
,则![]() ,易得
,易得![]() ,当且仅当
,当且仅当![]() 时取到,从而对一切
时取到,从而对一切![]() ,都有
,都有![]() 成立.
成立.
-
科目: 来源: 题型:
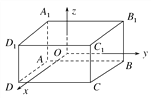
查看答案和解析>>【题目】如图,已知长方体ABCD-A1B1C1D1的对称中心在坐标原点,交于同一顶点的三个面分别平行于三个坐标平面,顶点A(-2,-3,-1),求其他七个顶点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,其中
,其中 为常数.
为常数. (1)判断函数
 的单调性并证明;
的单调性并证明;(2)当
 时,对于任意
时,对于任意 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正四棱锥P-ABCD中,底面边长为2,侧棱长为
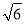 ,M,N分别为AB,BC的中点,以O为原点,射线OM,ON,OP分别为x轴、y轴、z轴的正方向建立空间直角坐标系.若E,F分别为PA,PB的中点,求A,B,C,D,E,F的坐标.
,M,N分别为AB,BC的中点,以O为原点,射线OM,ON,OP分别为x轴、y轴、z轴的正方向建立空间直角坐标系.若E,F分别为PA,PB的中点,求A,B,C,D,E,F的坐标.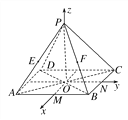
-
科目: 来源: 题型:
查看答案和解析>>【题目】【四川省高2017届第一次名校联考(广志联考)(理)】已知函数
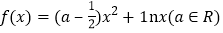 .
.(Ⅰ)当
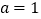 时,存在
时,存在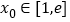 使不等式
使不等式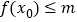 成立,求实数
成立,求实数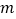 的取值范围;
的取值范围;(Ⅱ)若在区间
 上,函数
上,函数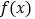 的图象恒在直线
的图象恒在直线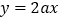 的下方,求实数
的下方,求实数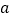 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知三点A(-1,1,2),B(1,2,-1),C(a,0,3),是否存在实数a,使A、B、C共线?若存在,求出a的值;若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数
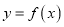 的导函数的图象如图所示,给出下列判断:
的导函数的图象如图所示,给出下列判断:①函数
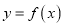 在区间
在区间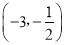 内单调递增;②函数
内单调递增;②函数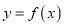 在区间
在区间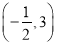 内单调递减;③函数
内单调递减;③函数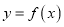 在区间
在区间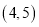 内单调递增;④当
内单调递增;④当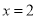 时,函数
时,函数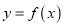 有极小值;⑤当
有极小值;⑤当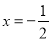 时,函数
时,函数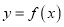 有极大值.则上述判断中正确的是( )
有极大值.则上述判断中正确的是( )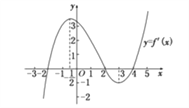
A. ①② B. ③
C. ②③ D. ③④⑤
相关试题

